To recap, multiple regression allows us to study the relationship between a dependent variable and multiple independent variables. The independent variables can be numerical (quantitative) or dummy (qualitative or categorical) variables. They can also be functions of independent variables, such as the curvature component and/or the interaction component. So how do we know what component to put into the multiple regression model?

You could always use trial and error - but that isn't good science. Formal techniques include forward selection (start with a simple linear regression model and add predictor variables as long as significant improvement is made); backward selection (start with a large pool of predictor variables and successively remove variables that do not significantly contribute to the prediction); stepwise regression (like forward selection but variables once added are also tested for removal after subsequent addition of more variables to determine if better models result); and best subsets (create subsets or combinations of all predictor variables and select the model with best statistical and practical utility). The Handbook of Parametric and Non parametric Statistical Procedures, by David Sheskin provides more details on the various methods.

The approach I would like you to use in Assignment 3 is a modification of the backward selection method. We will hypothesis a full multiple regression model with a quantitative independent variable, qualitative independent variable, curvature and interaction. We will then start taking components away that do not contribute to the statistical utility of the model. However, the way we take components away will be by following a decision tree in order to give us some structure.


In getting ready for Assignment 1, the first item is to enter your data into an Excel Spreadsheet, and create the curvature and interaction terms. I will demonstrate how to do this with several examples later in these notes. Item 2 requires that you build and test at least 2 of the hypothesized models shown in the next section, starting with Model 1 (Item 3 of Assignment 3).


Hypothesized Models

The decision tree will "walk us through" the selection of one of the following seven models that best fits the sample of data for your Assignment 3. The symbol QN stands for your quantitative X, QN² represents curvature, QL represents the qualitative X, and QN*QL represents interaction.

Model 1: E(Y) = B₀ + B₁ QN + B₂ QN² + B₃ QL + B₄ QN*QL

Model 2: E(Y) = B₀ + B₁ QN + B₃ QL + B₄ QN*QL

Model 3: E(Y) = B₀ + B₁ QN + B₂ QN² + B₃ QL

Model 4: E(Y) = B₀ + B₁ QN + B₂ QN²

Model 5: E(Y) = B₀ + B₁ QN + B₃ QL

Model 6: E(Y) = B₀ + B₃ QL

Model 7: E(Y) = B₀ + B₁ QN

A word description for each model is that the hypothesized regression model for predicting Y includes:

Model 1: Quantitative and qualitative variables, curvature and interaction

Model 2: Quantitative and qualitative variables, and interaction

Model 3: Quantitative and qualitative variables, and curvature

Model 4: A quantitative variable and curvature

Model 5: Quantitative and qualitative variables

Model 6: A qualitative variable

Model 7: A quantitative variable

Please note that there is no curvature term for the qualitative variable since categorical variables have no number properties beyond their 0/1 designation. To determine which model is best your sample data, we use the following decision tree.


Model Building Decision Tree

Item 3 in Assignment 3 asks you to run the Model 1 Regression Model. Item 4 in Assignment 3 requires that you first test to determine if curvature is important in that model. The decision tree then provides the actions you follow depending on the outcome of that and subsequent tests.

Item 4. Test curvature (Model 1 vs. 2).

A. If curvature is significant, test interaction (Model 1 vs. 3).

(1). If interaction is significant, stop. Model 1 is "best" model. Go to Item 5 (obtaining the residual, normal and line fit plots).

(2). If interaction is not significant, Build Model 3 and test QL (Model 3 vs. 4).

a. If QL is significant, stop. Model 3 is "best" model. Go to Item 5.

b. If QL is not significant, build Model 4 and stop. Model 4 is "best" model. Go to Item 5.

B. If curvature is not significant, build Model 2 and test interaction (Model 2 vs. 5).

(1). If interaction is significant, stop. Model 2 is "best" model. Go to item 5.

(2). If interaction is not significant, build Model 5 and test QL (Model 5 vs. 7).

a. If QL is significant, test QN (Model 5 vs. 6).

1. If QN is significant, stop. Model 5 is "best" model. Go to Item 5.

2. If QN is not significant, stop. Model 6 is "best model. Go to Item 5.

b. If QL is not significant, stop and select Model 7 as "best" model, even if the Model is not significant. Go to Item 5.

Although Item 5 is not part of the decision tree, it is part of the Assignment 3 requirement so I am repeating it here for ready reference (it and the Item 4 decision tree appear in the Main Module 3 Web Page).

5. Rerun the data analysis regression tool for your "best" model, and include and be able to describe or interpret the following printouts:

• Residual plot :
  • QN (Model 4 or 7)
  • QL Model 6)
  • QN and QL (Models 1, 2, 3, or 5)
• Normal probability plot (for all Models)
• Fitted Line Plot:
  • QN² (Models 1, 3, 4)
  • QN (Models 1, 2, 3, 4, 5, 7)
  • QL (Models 1, 2, 3, 5, 6)

Example One: Drug Effectiveness

Item 1: Enter Data
I am going to use as my first example, the study introduced at the end of Module Notes 3.2: the new drug effectiveness study data.

This example concerned an experiment done by an over-the-counter drug manufacturer interested in testing a new drug. This drug is designed to be effective in curing an illness most commonly found in older patients. The dependent variable is Effect, which stands for the effectiveness of recovery from a certain illness. It is measured on a scale of 0 to 100 (100 is more effective). The quantitative independent variable is age, and the qualitative independent variable is whether or not the new drug was present in the experiment (drug = 0) or absent (subjects took the old drug, drug = 1) in the experiment. Note that half of the subjects were given the new drug, and half were given the old drug (they were not told which one to avoid bias in the experiment).

Worksheet 3.3.1 shows the data entry (Item 1, Assignment 1).

Worksheet 3.3.1

Age	Age^2	Drug	Age*Drug	Effect
21	441	1	21	56
19	361	0	0	28
28	784	1	28	55
23	529	0	0	25
67	4489	0	0	71
33	1089	1	33	63
33	1089	1	33	52
56	3136	0	0	62
45	2025	0	0	50
38	1444	1	38	58
37	1369	0	0	46
27	729	0	0	34
43	1849	1	43	65
47	2209	0	0	59
48	2304	1	48	64
53	2809	1	53	61
29	841	0	0	36
53	2809	1	53	69
58	3364	1	58	73
63	3969	1	63	62
59	3481	0	0	71
51	2601	0	0	62
67	4489	1	67	70
63	3969	0	0	71

I entered the quantitative X, Age, in the first column. The second column is the curvature term which is constructed by squaring each value in the Age Column. The third column is the qualitative X, drug (0 = new drug was present, 1 = new drug was absent). The fourth column includes the interaction component, which is obtained by multiplying the respective cells in the Age Column times the cells in the Drug Column. I titled this Age*Drug to represent the multiplication. Finally, the last column contains the quantitative Y variable.

You are free to set up your data as you wish, the above format seems to be most efficient of the various formats I tried. Your requirement is similar to the example above: one quantitative X, one qualitative X, and a quantitative Y. Curvature and interaction are constructed.

Item 2: Build Model 1
Item 2, Assignment 3, requires that you hypothesize and run a full model with the quantitative and qualitative variables, curvature and interaction.

Worksheet 3.3.2 illustrates the regression summary from using the Regression Data Analysis Add In.

Worksheet 3.3.2

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.967077619
R Square	0.935239122
Adjusted R Square	0.921605253
Standard Error	3.888421114
Observations	24
ANOVA
	df	SS	MS	F	Significance F
Regression	4	4148.681777	1037.170444	68.59675111	5.04008E-11
Residual	19	287.2765564	15.11981876
Total	23	4435.958333
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	-0.05567568	7.441829412	-0.007481451	0.994108718	-15.63160849	15.52025713
Age	1.372995238	0.36799282	3.731038117	0.001415911	0.602777175	2.143213302
Age^2	-0.003978725	0.004228799	-0.940864063	0.358583821	-0.012829706	0.004872256
Drug	40.47038187	5.11462738	7.912674543	1.97194E-07	29.7653404	51.17542333
Age*Drug	-0.688569563	0.109012691	-6.316416545	4.6164E-06	-0.916735817	-0.460403308

Note: I do not recommend selecting any of the output options at this point. The Regression Summary is all that we need for the various component test procedures in the decision tree. Once we have our best model, we can rerun it and produce all of the output options such as residual, normal and line fit plots.

First Test: Curvature
Item 4, Assignment 3, requires that we test curvature. This is where the decision tree begins. Since we have the full Model 1 constructed, we can easily test for curvature by comparing Model 1 to Model 2. Model 2 is just like Model 1 except it doesn't have curvature.

The slope coefficient that we need to use to test curvature is B₂. The null and alternate hypotheses to test curvature are:

H₀: B₂ = 0 (curvature is not important)
H_a: B₂ =/= 0 (curvature is important)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 2, and the hypothesized model associated with the alternative hypothesis is Model 1:

Model 2 Associates with H₀: Effect = B₀ + B₁ Age + B₃ Drug +

B₄ Age*Drug

Model 1 Associates with H₁: Effect = B₀ + B₁ Age + B₂ Age² +

B₃Drug + B₄ Age*Drug

Since the p-value (0.35858) for the curvature term (Age^2) in Worksheet 3.3.2 is greater than alpha of 0.01, do not reject the null hypothesis, and conclude that curvature is not important. This means that Model 2 is a better predictor than Model 1. We need to rerun the regression without the curvature term, and next test interaction. This is noted in Decision Tree Action B.

Second Test: Interaction
To create a sample regression model for hypothesized Model 2, I remove the curvature column, and redo the regression analysis. The practice I follow is to make a copy of the original data to another worksheet tab or area on the current tab, and then delete the curvature column (or curvature data if I need information below the data in that column). If you delete the data, you need to shift the remaining data (qualitative, interaction and Y entries) to the left to keep all of the X variable columns adjacent to each other. The result is shown in Worksheet 3.3.3

Worksheet 3.3.3

Age	Drug	Age*Drug	Effect
21	1	21	56
19	0	0	28
28	1	28	55
23	0	0	25
67	0	0	71
33	1	33	63
33	1	33	52
56	0	0	62
45	0	0	50
38	1	38	58
37	0	0	46
27	0	0	34
43	1	43	65
47	0	0	59
48	1	48	64
53	1	53	61
29	0	0	36
53	1	53	69
58	1	58	73
63	1	63	62
59	0	0	71
51	0	0	62
67	1	67	70
63	0	0	71

Next I run the regression for Model 2. This is shown in Worksheet 3.3.4.

Worksheet 3.3.4

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.96551637
R Square	0.932221861
Adjusted R Square	0.92205514
Standard Error	3.87724774
Observations	24
ANOVA
	df	SS	MS	F	Significance F
Regression	3	4135.297333	1378.432444	91.69346477	7.33335E-12
Residual	20	300.6610008	15.03305004
Total	23	4435.958333
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	6.211381194	3.308965648	1.877136802	0.075164685	-0.690996989	13.11375938
Age	1.033390871	0.071447502	14.46363902	4.70078E-12	0.884354064	1.182427679
Drug	41.30421013	5.022786373	8.223365889	7.5975E-08	30.82686622	51.78155404
Age*Drug	-0.702883614	0.10763568	-6.530210205	2.30245E-06	-0.927407604	-0.478359625

Step B of the Decision Tree shows that to test interaction, we test Model 2 against Model 5. Similar to before, the only difference between these two Models is that Model 2 includes interaction, Model 5 does not. The slope coefficient associated with interaction is B₄. The null and alternative hypotheses to test interaction are:

H₀: B₄ = 0 (interaction is not important)

H_a: B₄ =/= 0 (interaction is important)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 5, and the hypothesized model associated with the alternative hypothesis is Model 2. Note that neither model has the curvature term since we already determined that curvature was not important and removed it.

Model 5 Associates with H₀: Effect = B₀ + B₁ Age + B₃ Drug

Model 2 Associates with H₁: Effect = B₀ + B₁ Age + B₃Drug

+ B₄ Age*Drug

Since the p-value (2.3E-06) for the interaction term (Age*Drug) in Worksheet 3.3.3 is less than alpha of 0.01, reject the null hypothesis, and conclude that interaction is important. This means that Model 2 is a better predictor than Model 5. Note in the decision tree action B (1), that if interaction is important at this point in the tree, we stop, Model 2 is our best model. You see, we do not need to test if the quantitative or if the qualitative variables are important, since if interaction is important, we need both the quantitative and qualitative variables to create it (the interaction).

Item 5: Assignment 3
Now that you have your best model, rerun the regression and select all of the output options of the regression add in dialog box (residual, normal, and line fit plots and standardized residuals). You are now ready to interpret the regression coefficients, test practical utility of your model, test statistical utility of your model, evaluate the assumptions and make a prediction.

The Sample Regression Equation and Interpretation of Coefficients
Worksheet 3.3.4 provides the coefficients for the sample regression equation:

Eq. 3.3.1: Effect = 6.2 + 1.03 Age + 41.3 Drug - 0.7Age*Drug

Since this is an interaction model, we have two interpretations for the slope and intercept. For the case where drug = 0 (new drug), the equation becomes:

Eq. 3.3.2: Effect = 6.2 + 1.03 Age

The intercept means that the Effectiveness score would be 6.2 for a person of age equals zero. Since there were no subjects at that age, the intercept would not have practical meaning. The slope suggests that when age increases by one, the effectiveness score increases by 1.03 (again, holding the qualitative variable constant at drug = 0).

For the case where drug = 1 (old drug), the equation becomes:

Eq. 3.3.3: Effect = 47.5 + 0.33 Age

The intercept now means that Effectiveness score would be 47.5 for a person of age equals zero. Since there were no subjects at that age, the intercept would not have practical meaning. The slope suggests that when age increases by one, the effectiveness score increases by 0.33 (again, holding the qualitative variable constant at drug = 1).

Practical Utility
The Adjusted R Square for this multiple regression model is shown as 0.92. The interpretation is that age and drug type explain 92% of the variation in effectiveness score. This is a high degree of variation explained. The Standard Error of the Model is 3.877, meaning that 95% of the actual effectiveness scores would be within +/- 2 * 3.877 = 7.75) of predicted effectiveness scores. This appears to be a relatively low standard error. The model is judged to be practically useful.

Statistical Utility
The following hypothesis test is used to determine model utility.

H₀: B₁ = B₃ = B₄ = 0 (regression model is not statistically useful)

H_a: At least one B =/= 0 (regression model is statistically useful)

Since the p-value (7.33E-12) for the F statistic in the Regression Row of the ANOVA table of Worksheet 3.3.4 is less than alpha of 0.01, reject the null hypothesis and conclude that the model is statistically useful.

Assumptions
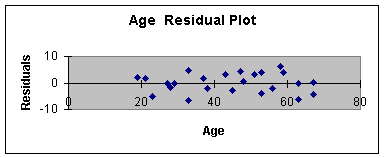
I examined the standardized residuals and the normal probability plot and found no outliers, indicating that the assumption that the error terms are normally distributed around a mean of zero can be considered met. To determine if we meet the assumptions that the error has constant variance and is independent, we examine the residual plots. There will be two plots since there are two independent variables. Worksheet 3.3.5 provides the residual plot Age, and Worksheet 3.3.6 provides the residual plot for Drug.

Worksheet 3.3.5



Worksheet 3.3.6


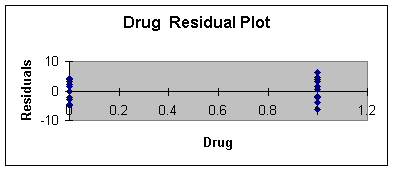
The plot of residual or errors against age shows fairly constant variance for all values of Age. Likewise, the errors plotted against drug shows about the same spread for drug = 0 and drug = 1.

Making a Prediction
To predict the effectiveness score for a new drug (drug = 0) administered a 63 year old, we first obtain the point estimate:

Eq. 3.3.4: Effect = 6.2 + 1.03Age + 41.3 Drug - 0.7 Age*Drug;

Effect = 6.2 + 1.03 (63) + 41.3 (0) -0.7 (63*0);
Effect = 6.2 + 64.9 = 71.1

Next, incorporate two times the standard error to get the 95% prediction interval:

Eq. 3.3.5: Effect = 71.1 +/- (2 * 3.877) = 71.1 +/- 7.75

We are 95% confident that a person 63 years of age, using the new drug, will have an effectiveness score between 63.35 and 78.85.


Example Two: Salary Study

Item 1: Enter Data
The second model building example concerns the Salary Study that was introduced in Module Notes 3.2 to illustrate the concepts of curvature, dummy variable, and interaction. I will use that example here to demonstrate how to determine the "best" model - that is, what combination of the the independent variables (quantitative variable, qualitative variable, curvature, and interaction) would best predict faculty salary.

The data that had to be collected includes faculty salary (dependent variable, Y), years of experience (quantitative independent variable, X₁), and gender (qualitative independent variable, X₂). The data that is created is for the curvature and interaction terms shown in Worksheet 3.3.7.

Worksheet 3.3.7

Years	Years^2	Gender	Yrs*Gndr	Salary
13	169	1	13	72000
13	169	0	0	68000
10	100	1	10	66000
10	100	0	0	64000
14	196	1	14	64000
8	64	1	8	62000
15	225	1	15	61000
11	121	0	0	60000
9	81	1	9	60000
15	225	0	0	59000
5	25	1	5	59000
12	144	1	12	59000
11	121	1	11	58000
6	36	0	0	57000
7	49	1	7	56000
12	144	0	0	55000
6	36	1	6	55000
9	81	0	0	52000
14	196	0	0	51000
7	49	0	0	50000
3	9	1	3	45000
3	9	0	0	44000
4	16	1	4	44000
4	16	0	0	42000
8	64	0	0	41000
5	25	0	0	34000
2	4	1	2	34000
1	1	1	1	30000
2	4	0	0	25000
1	1	0	0	22000

Item 2: Build Model 1
Worksheet 3.3.8 illustrates the regression summary from using the Regression Analysis Data Analysis Add In.

Worksheet 3.3.8

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.901285985
R Square	0.812316427
Adjusted R Square	0.782287055
Standard Error	6034.722055
Observations	30
ANOVA
	df	SS	MS	F	Significance F
Regression	4	3940519910	985129977.4	27.05073003	9.23118E-09
Residual	25	910446757.2	36417870.29
Total	29	4850966667
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	16652.01465	4452.309573	3.740084642	0.000962747	7482.317863	25821.71144
Years	6723.028442	1122.510607	5.98927832	2.96435E-06	4411.176191	9034.880693
Years^2	-268.1803491	66.43741887	-4.036585912	0.000450987	-405.0106787	-131.3500194
Gender	8619.047619	4637.228193	1.85866368	0.074886968	-931.4959304	18169.59117
Yrs*Gndr	-235.7142857	510.0271021	-0.462160314	0.647963296	-1286.13403	814.7054581

As with Example 1, I did not select any of the output Residual or Normal Probability Output options at this time since I am just building the model. Once we have the best model, we can rerun it and produce all of the output options at that time.

First Test: Curvature
Following the decision tree, our first test on Model 1, the full model that includes all of the hypothesized components, is for curvature.

The slope coefficient that we need to use to test curvature is B₂. The null and alternate hypotheses to test curvature are:

H₀: B₂ = 0 (curvature is not important)
H_a: B₂ =/= 0 (curvature is important)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 2, and the hypothesized model associated with the alternative hypothesis is Model 1:

Model 2 Associates with H₀: Salary= B₀ + B₁ Years + B₃ Gender +

B₄ Yrs*Gndr

Model 1 Associates with H₁: Salary = B₀ + B₁ Years + B₂ Years² +

B₃ Gender + B₄ Yrs*Gndr

Since the p-value (0.00045) for the curvature term (Years^2) in Worksheet 3.3.8 is less than alpha of 0.01, reject the null hypothesis, and conclude that curvature is important. This means that Model 1 is a better predictor than Model 2, and at this point, we keep Model 1 as our best model so far. We are at Item 4, A. in the decision tree. Note that the decision tree now tells us to test interaction by examining Model 1 vs. Model 3.

Second Test: Interaction
The only difference between Model 1 and Model 3 is that Model 1 includes interaction, Model 3 does not. Note that both models include curvature since we previously determined that curvature is important in predicting salary. The slope coefficient associated with interaction is B₄. The null and alternative hypotheses to test interaction are:

H₀: B₄ = 0 (interaction is not important)

H_a: B₄ =/= 0 (interaction is important)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 3, and the hypothesized model associated with the alternative hypothesis is Model 1. Note that both models include curvature.

Model 3 Associates with H₀: Salary= B₀ + B₁ Years + B₂ Years² +

B₃ Gender

Model 1 Associates with H₁: Salary= B₀ + B₁ Years + B₂ Years² +

B₃ Gender + B₄ Yrs*Gndr

Since the p-value (0.647963) for the interaction term (Yrs*Gndr) in Worksheet 3.3.8 is greater than alpha of 0.01, do not reject the null hypothesis, and conclude that interaction is not important. This means that Model 3 is a better predictor than Model 1. Note in the decision tree Item A (2), that if interaction is not important, build Model 3 and test for the importance of the qualitative variable. We need to rerun the regression without the interaction term to create Model 3.

Third Test: Qualitative Variable
To build Model 3, I remove the interaction column and redo the regression analysis. The result is shown in Worksheet 3.3.9.

Worksheet 3.3.9

Years	Years^2	Gender	Salary
13	169	1	72000
13	169	0	68000
10	100	1	66000
10	100	0	64000
14	196	1	64000
8	64	1	62000
15	225	1	61000
11	121	0	60000
9	81	1	60000
15	225	0	59000
5	25	1	59000
12	144	1	59000
11	121	1	58000
6	36	0	57000
7	49	1	56000
12	144	0	55000
6	36	1	55000
9	81	0	52000
14	196	0	51000
7	49	0	50000
3	9	1	45000
3	9	0	44000
4	16	1	44000
4	16	0	42000
8	64	0	41000
5	25	0	34000
2	4	1	34000
1	1	1	30000
2	4	0	25000
1	1	0	22000

Next, I run the regression for Model 3. This is shown in Worksheet 3.3.10.

Worksheet 3.3.10

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.900395978
R Square	0.810712917
Adjusted R Square	0.7888721
Standard Error	5942.756834
Observations	30
ANOVA
	df	SS	MS	F	Significance F
Regression	3	3932741338	1310913779	37.11916585	1.52134E-09
Residual	26	918225328.6	35316358.79
Total	29	4850966667
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	17594.87179	3897.092239	4.514871785	0.000120961	9584.278723	25605.46487
Years	6605.171299	1076.50067	6.135780016	1.73624E-06	4392.391031	8817.951568
Years^2	-268.1803491	65.42495602	-4.099052799	0.000360926	-402.6633603	-133.6973378
Gender	6733.333333	2169.987981	3.102935773	0.004577524	2272.856233	11193.81043

To test for the importance of the qualitative variable at this point in the decision tree process (Item 4.A.(2).), we compare Model 3 with Model 4. The only difference between these two models is that Model 3 includes the qualitative variable, Model 4 does not. Note that both models include curvature, and neither model includes interaction, which follows from the testing done so far. The slope coefficient associated with the qualitative variable is B₃. The null and alternative hypotheses to test for the qualitative variable are:

H₀: B₃ = 0 (qualitative variable, gender, is not important)
H_a: B₃ =/= 0 (gender is important in predicting salary)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 4, and the hypothesized model associated with the alternative hypothesis is Model 3:

Model 4 Associates with H₀: Salary= B₀ + B₁ Years + B₂ Years²

Model 3 Associates with H₁: Salary = B₀ + B₁ Years + B₂ Years² +

B₃ Gender

Since the p-value (0.004578) for the qualitative term (Gender) in Worksheet 3.3.10 is less than alpha of 0.01, reject the null hypothesis, and conclude that gender is important in predicting salary. This means that Model 3 is a better predictor than Model 4, and at this point, we keep Model 3 as our best model so far. We are at Item 4, A. (2).a. in the decision tree. Note that the decision tree now tells us to stop, we have arrived at our best model. Since curvature is important, there is no need to test the quantitative variable, Years, since Years is needed to make the curvature term. That is why the decision tree said to stop.

Item 5: Assignment 3
Now that we have the best model, rerun the regression and select all of the output options of the Regression Add In dialog box (residual, normal and line fit plots and standardized residuals). You are now ready to interpret the regression coefficients, test practical utility of your model, test statistical utility of your model, evaluate the assumptions, and make a prediction.

The Sample Regression Equation and Interpretation of the Coefficients
Worksheet 3.3.10 provides the coefficients for the sample regression equation:

Eq. 3.3.6: Salary = 17595 + 6605 Years - 268 Years² +

6733 Gender

Since this model includes gender, we will have two equations, one for male faculty members (X₂ = 1) and one for female faculty members (X₂ = 0). The equation for male faculty members is:

Eq. 3.3.7: Salary = 14328 + 6605 Years - 268 Years²

The equation for female faculty members is:

Eq. 3.3.8: Salary = 17595 + 6605 Years - 268 Years²

Thus, the slope coefficient on gender, B₃ = 6733 in Equation 3.3.6, is the average difference in salary between males and females: males make $6,733 average more than females. This is a case of gender discrimination since the faculty were similar in all other regards.

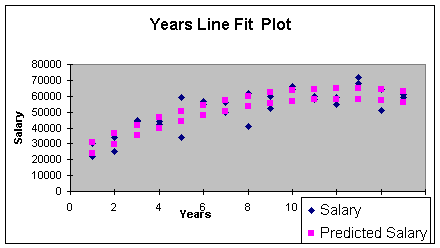
The other slope of interest to us is B₂, the slope on the curvature term. Its value is -268. About all that we can say from a management interpretation, is that the negative term means we have negative or downward curvature. This means that as experience increases, salary increases but at a decreasing rate. A glimpse at the line fit plot illustrates the above discussion. This plot is shown in Worksheet 3.3.11. Note the two curves, the top being the predicted salary curve for male faculty, the bottom curve for female faculty. The salary curve is typical in a public university as faculty get promoted to associate and then full professor by the 10 - 15 year point, then follow-on raises follow small incremental state yearly increases. What should not be typical is the two curves as that is discrimination if all other factors are the same.

Worksheet 3.3.11

Practical Utility
The adjusted R Square is 0.81 meaning that years experience and gender explain 81% of the sample variation in salary in this curvilinear model. This is a high degree of explained variation. The Standard Error of the Model is $5,943. which is interpreted to be 95% of the actual salaries will be within +/- 2 * $5,943 or +/- $11,846 of the predicted salaries. This error is obviously too high for prediction purposes, but if the model was to be used solely to understand the discrimination effect, it might be acceptable. I should add a caution here. You may have noticed that there were just 30 observations in this example. There should have been a minimum of 50. If we used the larger minimum number of observations, the standard error should improve (remember standard errors and standard deviations reduce as you increase sample size to the minimum required).

Statistical Utility
The following hypothesis test is used to determine model utility.

H₀: B₁ = B₂ = B₃ = 0 (regression model is not statistically useful)
H_a: At least one B =/= 0 (model is statistically useful)

Since the p-value (1.52E-09) for the F statistic in the Regression Row of the ANOVA table of Worksheet 3.3.10 is less than alpha of 0.01, reject the null hypothesis and conclude that the model is statistically useful.

Assumptions
I examined the standardized residuals and the normal probability plot and found no outliers, indicating that the assumption that the error terms are normally distributed around a mean of zero can be considered met. To determine if we meet the assumptions that the error has constant variance and is independent, we examine the residual plots.

There will be two plots of interest, the plot for the quantitative X and the plot for the qualitative X. You will also get a plot for the curvature term but this is a derived variable and may be ignored. Assignment 3, Step 5, in the Main Module 3 Notes and repeated at the beginning of this note set states exactly what residual plots you need according to which model number is your best model. 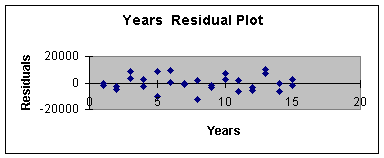Worksheet 3.3.12 provides the residual plot for Years, and Worksheet 3.3.13 provides the residual plot for gender.

Worksheet 3.3.12



Worksheet 3.3.13



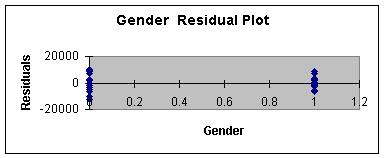
The Years Residual Plot shows very little error for 1, 2, 14, and 15 years of experience compared to 5 and 7. As well, the male gender residual is smaller than the female residual. This is a second indication of a small sample size problem. A larger sample size should even out the distribution of the error for all values of the independent variables.

Making a Prediction
To predict the salary for the first female faculty member in our data set (13 years experience), we first obtain the point estimate:

Eq. 3.3.9: Salary = 17595 + 6605 Years - 268 Years² +

6733 Gender;

Salary = 17595 + 6605 (13) - 268 (13)² +

6733 (0);

Salary = $58,168

Next, incorporate the standard error to get a 95% prediction interval:

Eq. 3.3.10: Salary = 58168 +/- (2 * 5943) = 58168 +/- 11886.

So, we are 95% confident that a female faculty member with 13 years experience will make between $46,282 and $70,054. As indicated earlier, that is a wide range for prediction purposes. Perhaps more data or stratification of the faculty by years of experience would produce a model with less error.

The error of prediction for this particular observation is actual minus predicted which is 68,000 - 58,186 or $9,814.


Example Three: External Hour/Asset Study

For the last example, I picked a problem where I knew there was no curvature, interaction or significant quantitative variable - just a simple linear regression. This is the example I used for Module Notes 2.1 and 2.2 .

Item 1: Enter Data
The data for this problem involves a quantitative independent variable, Assets in thousands of dollars; a qualitative independent variable, years of experience (Exp) of the audit team leader; and the dependent variable, External Hours to do an audit. Please note that experience was actually a quantitative variable. I made it into a dummy variable by noting that 1 = team leader with years of experience greater than 5, and 0 = years of experience less than or equal to 5. You can make quantitative variables dummy variables, but not the other way around. Worksheet 3.3.14 provides the data input.

Worksheet 3.3.14

Assets	Assets^2	Exp	Asset*Exp	ExtHours
3200	10240000	1	3200	700
3000	9000000	1	3000	900
3500	12250000	1	3500	800
4000	16000000	1	4000	900
4700	22090000	1	4700	880
5000	25000000	1	5000	850
6000	36000000	0	0	1000
5500	30250000	0	0	1000
6500	42250000	1	6500	950
6500	42250000	0	0	1100
7000	49000000	0	0	1200
4500	20250000	1	4500	830
7500	56250000	0	0	1100
5750	33062500	1	5750	1100
7250	52562500	0	0	1160
8000	64000000	1	8000	1120
8000	64000000	0	0	1300
8500	72250000	0	0	1400
9000	81000000	1	9000	1500
8500	72250000	0	0	1200

Item 2: Build Model 1
Worksheet 3.3.15 illustrates the regression summary from using the Regression Analysis Data Analysis Add In.

Worksheet 3.3.15

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.927239544
R Square	0.859773172
Adjusted R Square	0.822379352
Standard Error	87.51652745
Observations	20
ANOVA
	df	SS	MS	F	Significance F
Regression	4	704407.8613	176101.9653	22.99239	2.97E-06
Residual	15	114887.1387	7659.142577
Total	19	819295
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	1214.943829	443.3511933	2.740364405	0.015177	269.9625	2159.925
Assets	-0.129373898	0.115830849	-1.116920912	0.2816	-0.376262	0.117514
Assets^2	1.66433E-05	7.90665E-06	2.104978726	0.05256	-2.09E-07	3.35E-05
Exp	-248.8972384	268.8201043	-0.925887739	0.369162	-821.8741	324.0796
Asset*Exp	0.030084261	0.037500954	0.802226542	0.434948	-0.049847	0.110016

First Test: Curvature
Following the decision tree, our first test on Model 1 is for curvature. The slope coefficient that we need to use to test curvature is B₂. The null and alternative hypotheses to test curvature are:

H₀: B₂ = 0 (curvature is not important)

H_a: B₂ =/= 0 (curvature is important)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 2, and the hypothesized model associated with the alternative hypothesis is Model 1:

Model 2 Associates with H₀: ExtHours = B₀ + B₁ Assets +

B₃ Exp + B₄ Assets*Exp

Model 1 Associates with H₁: ExtHours = B₀ + B₁ Assets +

B₂ Assets² + B₃ Exp + B₄ Assets*Exp

Since the p-value (0.05256) for the curvature term (Years^2) in Worksheet 3.3.14 is greater than 0.01, we fail to reject the null hypothesis and conclude that curvature is not important. At this point, Model 2 is our best model - we are at Item 4.B. in the decision tree. We need to remove curvature from the data set, build Model 2, and prepare for the interaction test.

Second Test: Interaction
Worksheet 3.3.16 illustrates the data with the curvature term removed.

Worksheet 3.3.16

Assets	Exp	Asset*Exp	ExtHours
3200	1	3200	700
3000	1	3000	900
3500	1	3500	800
4000	1	4000	900
4700	1	4700	880
5000	1	5000	850
6000	0	0	1000
5500	0	0	1000
6500	1	6500	950
6500	0	0	1100
7000	0	0	1200
4500	1	4500	830
7500	0	0	1100
5750	1	5750	1100
7250	0	0	1160
8000	1	8000	1120
8000	0	0	1300
8500	0	0	1400
9000	1	9000	1500
8500	0	0	1200

Next, I run the regression for Model 2. This is shown in Worksheet 3.3.17.

Worksheet 3.3.17

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.904627421
R Square	0.818350771
Adjusted R Square	0.784291541
Standard Error	96.44438323
Observations	20
ANOVA
	df	SS	MS	F	Significance F
Regression	3	670470.6951	223490.2317	24.02728	3.62E-06
Residual	16	148824.3049	9301.519057
Total	19	819295
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	395.5572755	233.8658163	1.691385607	0.110145	-100.216	891.3305
Assets	0.106563467	0.032197854	3.309645011	0.004428	0.038307	0.17482
Exp	57.03551305	249.2139422	0.228861646	0.821876	-471.2743	585.3454
Asset*Exp	-0.009424722	0.035777859	-0.263423299	0.795587	-0.08527	0.066421

Step B of the Decision Tree shows that to test interaction, we test Model 2 against Model 5. Similar to before, the only difference between these two Models is that Model 2 includes interaction, Model 5 does not. The slope coefficient associated with interaction is B₄. The null and alternative hypotheses to test interaction are:

H₀: B₄ = 0 (interaction is not important)

H_a: B₄ =/= 0 (interaction is important)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 5, and the hypothesized model associated with the alternative hypothesis is Model 2. Note that neither model has the curvature term since we already determined that curvature was not important and removed it.

Model 5 Associates with H₀: ExtHours = B₀ + B₁ Assets + B₃ Exp

Model 2 Associates with H₁: ExtHours = B₀ + B₁ Assets + B₃ Exp

+ B₄ Assets*Exp

Since the p-value (0.795587) for the interaction term (Assets*Exp) in Worksheet 3.3.17 is greater than alpha of 0.01, do not reject the null hypothesis, and conclude that interaction is not important. This means that Model 5 is a better predictor than Model 2. Note in the decision tree Step 4.B. (2), that we now must build Model 5 by removing interaction from the data set. We then will test if the qualitative dummy variable is important.

Third Test: Qualitative Variable
Worksheet 3.3.18 illustrates the data with the interaction term removed.

Assets	Exp	ExtHours
3200	1	700
3000	1	900
3500	1	800
4000	1	900
4700	1	880
5000	1	850
6000	0	1000
5500	0	1000
6500	1	950
6500	0	1100
7000	0	1200
4500	1	830
7500	0	1100
5750	1	1100
7250	0	1160
8000	1	1120
8000	0	1300
8500	0	1400
9000	1	1500
8500	0	1200

Next, I run the regression for Model 5. This is shown in Worksheet 3.3.19.

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.904191882
R Square	0.81756296
Adjusted R Square	0.796099779
Standard Error	93.76747033
Observations	20
ANOVA
	df	SS	MS	F	Significance F
Regression	2	669825.2456	334912.6228	38.09142	5.24E-07
Residual	17	149469.7544	8792.338493
Total	19	819295
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	450.472272	103.0525338	4.371287684	0.000416	233.0501	667.8944
Assets	0.098930495	0.013649179	7.248091277	1.36E-06	0.070133	0.127728
Exp	-7.188434707	50.20635226	-0.143177793	0.887833	-113.1147	98.73786

Step 4.B.(2) of the Decision Tree shows that to test for the importance of the qualitative variable, we test Model 5 against Model 7. Similar to before, the only difference between these two Models is that Model 5 includes the qualitative variable, Model 7 does not. The slope coefficient associated with the qualitative variable is B₃. The null and alternative hypotheses to test interaction are:

H₀: B₃ = 0 (qualitative variable, Exp, is not important)

H_a: B₃ =/= 0 (Exp is important in predicting ExtHours)

The hypothesized model associated with the null hypothesis at this point in the decision tree is Model 7, and the hypothesized model associated with the alternative hypothesis is Model 5. Note that neither model has the curvature or interaction terms since we already determined that curvature and interaction were not important and removed them from further model consideration.

Model 7 Associates with H₀: ExtHours = B₀ + B₁ Assets

Model 5 Associates with H₁: ExtHours = B₀ + B₁ Assets + B₃ Exp

Since the p-value (0.887833) for the qualitative variable (Exp) in Worksheet 3.3.19 is greater than alpha of 0.01, do not reject the null hypothesis, and conclude that the qualitative variable is not important. This means that Model 7 is a better predictor than Model 5. Note in the decision tree Step 4.B. (2) b., that we now must build Model 7 by removing the qualitative variable from the data set. We then build a new regression analysis and stop (this is for test purposes - if you get to this point in the decision tree, Model 7 will be considered your "best" model so you will have something to analyze for the exam - this is true even if your Model 7 has no statistical utility).

Build Model 7: Simple Linear Regression Model with Quantitative Variable

Worksheet 3.3.20 provides the simple linear regression data for Model 7.

Assets	ExtHours
3200	700
3000	900
3500	800
4000	900
4700	880
5000	850
6000	1000
5500	1000
6500	950
6500	1100
7000	1200
4500	830
7500	1100
5750	1100
7250	1160
8000	1120
8000	1300
8500	1400
9000	1500
8500	1200

Next, we run the regression analysis with residual output, residual plot, line fit plot and normal probability plot. These are used to evaluate practical utility, statistical utility, the assumptions, and to make the prediction.


That's it. I hope these three examples provide a "feel" for model building. You will learn more about it as you build your model for Assignment 3. Remember that these three examples illustrate a Model 2, a Model 3 and a Model 7 - you may have one of the models not illustrated as your best model.



References:


Sheskin, David J. (2000). Handbook of Parametric and Non Parametric Statistical Procedures (2nd. ed.). Boca Raton, FL: CRC Press LLC, Test 28.

Levine, D., Berenson, M. & Stephan, D. (1999). Statistics for Managers Using Microsoft Excel (2nd. ed.). Upper Saddle River, NJ: Prentice-Hall.

Chapter 14 -- Multiple Regression Models

Mason, R., Lind, D. & Marchal, W. (1999). Statistical Techniques in Business and Economics (10th. ed.). Boston: Irwin McGraw Hill.

Chapter 13 -- Multiple Regression and Correlation Analysis