In Module Notes 4.4, we introduced ANOVA as a powerful tool that allows us to compare samples of multiple groups and make conclusions concerning the equality of the population mean on one dimension or factor. The example we used was comparing mean mile per gallon performance (the outcome measure) for automobiles tested with different brands of gasoline (the factor). The factor, brand of gas, has three levels, Brand A, B and C.

In this set of notes, we expand the ANOVA concept to the examination of situations involving two factors. In the above example, perhaps we want to test mean mile per gallon performance for automobiles tested with different brands of gasoline (factor A) as well as different driving conditions (factor B). The different driving conditions might be city versus highway driving.

In this scenario, if there was a significant brand effect, then we would know that mean mpg performances groups differ with respect to at least two of the the three levels of the brand factor. Likewise, if there was a significant driving condition, then we would know the mean mpg performances differ with respect to the two levels of the driving condition factor.

But wait a minute, you say! Back in multiple regression when we had two independent variables, we also were concerned about interaction. Same thing holds true in Two- Factor ANOVA. Interaction here would mean that we would have to be concerned about mean mpg performance at six combination levels of the brand and driving condition factors. That is, mean mpg for city driving with Brand A, mean mpg for city driving with Brand B, mean mpg for city driving with Brand C, mean mpg for highway driving with Brand A, mean mpg for highway driving with Brand B, and mean mpg for highway driving with Brand C.

That's the idea - I want to present two example situations, one with interaction, and one without.


A Situation with Interaction

This example is from a utility company that was experimenting with variable pricing. Two factors are involved. The first is the length of the peak period. At the long peak situation (7 am - 7 p.m.), customers would have a 12 hour discount period between 7 p.m. and 7 am. At the short peak situation (8 am - 5 p.m.), customers would enjoy a 14 hour discount period between 5 p.m. and 8 am. The other factor is ratio of the discount. A low ratio is approximately a 2:1 discount on rates during off-peak usage. A high ratio is approximately a 3:1 discount on rates during off-peak usage.

The company prepared a satisfaction survey and measured satisfaction on a 50 point scale (50 being high satisfaction, 0 being low). The scores for a trial run of the survey are shown in Worksheet 4.5.1.

Worksheet 4.5.1

	Low Ratio	High Ratio
Long Peak	25	24
Long Peak	26	25
Long Peak	28	28
Long Peak	27	26
Short Peak	22	30
Short Peak	25	26
Short Peak	20	31
Short Peak	21	27

Worksheet 4.5.1 presents the data as you would enter it in an Excel Worksheet in preparation for running a Two-Factor ANOVA.

To run the ANOVA, select Tools from the Standard Toolbar, then Data Analysis from the pulldown menu, then ANOVA: Two-Factor with Replication. The dialog box is similar to those you have seen before. I highlight all of the data in the three columns and nine rows (including the labels) shown in Worksheet 4.5.1, and remembered to check Labels. Note an additional question, "Rows per sample." This is asking how many observations are in each of the two levels of the row factor, Long/Short Peak. Place "4" in the adjacent dialog box.

The ANOVA output is shown in Worksheet 4.5.2.

Worksheet 4.5.2

Anova: Two-Factor With Replication
SUMMARY	Low Ratio	High Ratio	Total
Long Peak
Count	4	4	8
Sum	106	103	209
Average	26.5	25.75	26.125
Variance	1.666667	2.916666667	2.125
Short Peak
Count	4	4	8
Sum	88	114	202
Average	22	28.5	25.25
Variance	4.666667	5.666666667	16.5
Total
Count	8	8
Sum	194	217
Average	24.25	27.125
Variance	8.5	5.839285714
ANOVA
Source of Variation	SS	df	MS	F	P-value	F crit
Sample	3.0625	1	3.0625	0.821229	0.382657	4.747221
Columns	33.0625	1	33.0625	8.865922	0.011538	4.747221
Interaction	52.5625	1	52.5625	14.09497	0.002749	4.747221
Within	44.75	12	3.729167
Total	133.4375	15

The first thing we get are the group means and variances. Note that the average satisfaction scores are 26.5 for the group long peak, low ratio; 25.75 for long peak, high ratio; 22 for short peak, low ratio; and 28 for short peak, high ratio. Worksheet 4.5.3 shows a picture of these means.

Worksheet 4.5.3
 
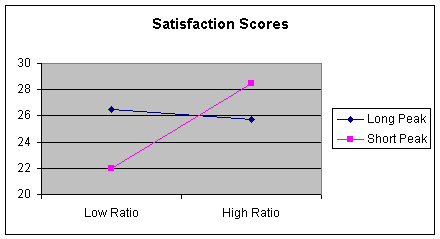
This is interesting data and shows interaction. Customer satisfaction depends upon the what combination of ratio and peak the customer was considering. In multiple regression, when interaction is present, we say the relationship between customer satisfaction and low or high ratio depends on length of the peak.

Statistically, to validate the presence of interaction, we examine the ANOVA table in Worksheet 4.5.2. There are three rows of interest. The Sample row pertains to variation attributed to the peak factor; the Column row pertains to variation attributed to the ratio factor; the Interaction row pertains to variation attributed to the interaction of combinations of both peak and ratio factors; and the Within row pertains to within group variation (variation unexplained by peak period or ratio discount).

The first thing we test for is interaction in the Two-Factor ANOVA model. The hypotheses are:

H₀: There is no interaction (Interaction is not important)
H_a: There is interaction (relationship between satisfaction and length of peak period depends on ratio discount; which is the same as stating the relationship between satisfaction and ratio discount depends on length of peak period).

Since the p-value for Interaction (0.002749) is less than an alpha value of 0.01 (I am using the lower value of alpha to recognize that we are doing multiple tests with the same data), we reject the null hypothesis and conclude there is interaction in the data. Thus, the company needs to consider both the length of the peak period as well as the discount ratio when setting peak/off peak price discounts.


A Situation without Interaction

A production firm that assembles surgical kits for hospital operating rooms noticed that female employees seem to assemble kits faster than male employees (this factor would be the gender factor). If there is a significant gender effect, the company would need to somehow recognize and respond to the different average assembly times. There is another factor that must be considered: there are two methods of assembly.

In this situation, the ANOVA model is used to determine if we can analyze average assembly time with respect to each factor independent of the other, or if we have to address interaction. If there is no interaction, the the average assembly time for males can be compared to the average assembly time for females . Likewise, if there is no interaction, then the average assembly time for Method 1 can be compared to the average assembly time for Method 2. If there is interaction, then averages involving combinations of the two factors must be studied: average assembly time for males using Method 1; for males using Method 2; for females using Method 1, and for females using Method 2. Worksheet 4.5.4 provides the data for running the Two-Factor ANOVA model in Excel.

Worksheet 4.5.4

	Method 1	Method 2
Male	125	121
Male	117	119
Male	123	120
Female	106	102
Female	107	102
Female	100	103

The Two-Factor ANOVA is run in Excel as before. Select Tools, Data Analysis, ANOVA: Two-Factor with Replication, and respond to the dialog box. This time, there are three rows for the Sample or row factor, Gender. Worksheet 4.5.5 provides the result.

Worksheet 4.5.5

Anova: Two-Factor With Replication
SUMMARY	Method 1	Method 2	Total
Male
Count	3	3	6
Sum	365	360	725
Average	121.6667	120	120.8333
Variance	17.33333	1	8.166667
Female
Count	3	3	6
Sum	313	307	620
Average	104.3333	102.3333333	103.3333
Variance	14.33333	0.333333333	7.066667
Total
Count	6	6
Sum	678	667
Average	113	111.1666667
Variance	102.8	94.16666667
ANOVA
Source of Variation	SS	df	MS	F	P-value	F crit
Sample	918.75	1	918.75	111.3636	5.67E-06	5.317645
Columns	10.08333	1	10.08333	1.222222	0.301061	5.317645
Interaction	0.083333	1	0.083333	0.010101	0.922417	5.317645
Within	66	8	8.25
Total	994.9167	11

Also as before, with Two-Factor Anova, we first test interaction. The hypotheses are:

H₀: There is no interaction (Interaction is not important)
H_a: There is interaction (relationship between assembly time and gender depends on assembly method; which is the same as stating the relationship between assembly time and assembly method depends on gender).

Since the p-value (0.922417) is greater than 0.01, we do not reject the null hypothesis and conclude there is no interaction.

Now we can independently test the factors. First, let's look at gender.

H₀: Mean_Male = Mean_Female
H_a: Mean_Male =/= Mean_Female

Since the p-value for the Sample Factor (the row or gender factor) (5.67E-06) is less than 0.01, reject the null hypothesis and conclude that the means are not equal. In this case, we can use the top part of the ANOVA result to see which mean is less. The Male mean is given in the total column for the Male data as 120.83 minutes per surgical kit, and for the Female data, the mean is 103.3. The females are significantly faster, on average, than the males.

Finally, we can test the assembly method factor. The hypotheses statements are:

H₀: Mean_{Method 1} = Mean_{Method 2}

H_a: Mean_{Method 1} =/= Mean_{Method 2}

Since the p-value (0.301061) for the Method factor (the Column factor), is greater than 0.01, do not reject the null hypothesis. These is no significant difference in the average assembly time for Method 1 compared to Method 2.

The company can now study the gender factor without regard to method of assembly. Here is a picture of this situation:

Worksheet 4.5.6


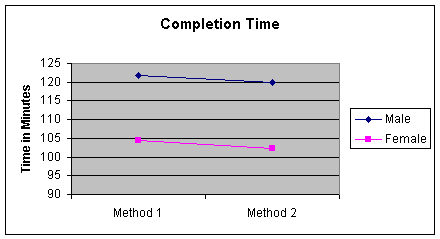
Note that the male averages are greater than the female averages, no matter what the method of assembly - that is a picture of no interaction.


Two-Factor Anova: Without Replication

You may have noticed that you have two choices in the Data Analysis selections for Two-Factor ANOVA. One is with replication (multiple rows for the factors being analyzed as we saw in both of the previous examples), and one without replication. The "without replication" can be used for problems such as the following.

A company employs three estimators in preparing bids for four different types of construction jobs. The company is interested in determining if the estimators are consistent in their bids. An experiment is created to have each estimator independently prepare an estimate for Job 1, Job 2, Job 3 and Job 4. So Estimator 1 prepares an estimate for Job 1, Estimator 2 prepares an estimate for Job 1, and Estimator 3 prepares an estimate for Job 1; this is repeated for Job 2, then Job 3, then Job 4.

The results are shown in Worksheet 4.5.7. Estimates are in millions of dollars.

Worksheet 4.5.7

	Estimator 1	Estimator 2	Estimator 3
Job 1	4.6	4.9	4.1
Job 2	6.2	6.3	5.6
Job 3	5	5.4	5.1
Job 4	6.6	6.8	6.0

To analyze this problem with Two-Factor ANOVA, we select Tools, Data Analysis, Anova: Two-Factor without Replication, fill-in the entries on the dialog box, and obtain the following output:

Worksheet 4.5.8

Anova: Two-Factor Without Replication
SUMMARY	Count	Sum	Average	Variance
Job 1	3	13.6	4.533333333	0.163333333
Job 2	3	18.1	6.033333333	0.143333333
Job 3	3	15.5	5.166666667	0.043333333
Job 4	3	19.4	6.466666667	0.173333333
Estim'r 1	4	22.4	5.6	0.906666667
Estim'r 2	4	23.4	5.85	0.736666667
Estim'r 3	4	20.8	5.2	0.673333333
ANOVA
Source of Variation	SS	df	MS	F	P-value	F crit
Rows	6.763333333	3	2.254444444	72.46428571	4.1954E-05	4.757055194
Columns	0.86	2	0.43	13.82142857	0.005672508	5.143249382
Error	0.186666667	6	0.031111111
Total	7.81	11

The hypothesis test of interest is as follows:

H₀: Mean_{Estimator 1} = Mean_{Estimator 2} = Mean_{Estimator 3}
H_a: At least two means are not equal

The factor of interest is Estimator, the column factor. Since the p-value (0.005672508) is less than alpha of 0.05 (only one test is being done with the data), we do reject the null hypothesis and conclude that there is a significant difference in the mean estimates. This finding would have to be addressed by management .

This model takes into consideration the fact that the jobs themselves had variability - Type 1 Jobs are smaller than Type 4 Jobs, for example. The Two-Factor ANOVA model without replication accounts for the variability of the row factor so that the column factor can be more effectively studied.

If we would have assumed that there is no difference in the job types, then we would assumed that jobs were independently and randomly assigned to each estimator. This is the One-Factor ANOVA we studied in Module Notes 4.4. Worksheet 4.5.9 shows the results of the One-Factor ANOVA.

Worksheet 4.5.9

Anova: Single Factor
SUMMARY
Groups	Count	Sum	Average	Variance
Estim'r 1	4	22.4	5.6	0.906666667
Estim'r 2	4	23.4	5.85	0.736666667
Estim'r 3	4	20.8	5.2	0.673333333
ANOVA
Source of Variation	SS	df	MS	F	P-value	F crit
Between Groups	0.86	2	0.43	0.556834532	0.591564315	4.256492048
Within Groups	6.95	9	0.772222222
Total	7.81	11

Note carefully that the p-value for Between Group variation (the Estimator factor) is now greater than 0.05, so we would not reject the null hypothesis and conclude the average estimates are the same. In this case, the wrong model would lead us to an erroneous conclusion.


Summary

The two factor ANOVA models are very powerful additions to the Single Factor ANOVA. The assumptions with the two-factor models are that populations from which the samples were drawn are normal and the variances are equal. The normality assumption is not critical in the presence of large sample sizes, and the variance assumption is not critical when there are equal sample sizes for the factor level combinations. However, when we work with small samples, samples with unequal sizes in the factor level combinations, and/or when the sample indicates extreme values (skewed data), we should revert to nonparametric techniques, as will be described in Module Notes 4.6.

The two-factor ANOVA with replication assumes that observations are randomly and independently assigned to each group of the two factors. The two-factor ANOVA does not make that assumption and is used when one wants to control for the variability of the row factor.


Readings:


Levine, D., Berenson, M. & Stephan, D. (1999). Statistics for Managers Using Microsoft Excel (2nd. ed.). Upper Saddle River, NJ: Prentice-Hall, Chapter 10.

Mason, R., Lind, D. & Marchal, W. (1999). Statistical Techniques in Business and Economics (10th. ed.). Boston: Irwin McGraw Hill, Chapter 11.