We now return to our study of numerical data. Recall in Module 1, we studied descriptive and inferential statistics involving the analysis of a single sample of numerical data. You may remember that the mean and standard deviation are measures of center and spread for symmetric bell-shaped or normally distributed data, and that the median and interquartile range are good measures of center and spread for skewed or otherwise non-normal data.

This module expands the study of numerical data to the situation where we want to study and compare two or more samples. Typically, we are interested in comparing the two or more samples to make an inference about the multiple populations from which they were drawn. We may ask questions such as, "is the mean of the first group equal to the mean of the second group?" Does my Internet Statistics class have higher average scores than my on-campus class (of course!). Do males employees make more money, on average, than female employees?

Do you recall that we asked that last question when we introduced categorical variables in Multiple Regression? In fact, multiple regression is one tool that can be used to study whether or not two or more means are equal - that is one reason I like to cover this topic after Regression.

The first three module notes (4.1 - 4.3) present situations in which we are interested in comparing the means of two samples. Along the way, we will also look at a way to compare the variances of two samples. Module Notes 4.4 - 4.6 then look at situations in which we are interested in comparing the means of many samples. This material is used quite a bit in data analysis - any time you want to compare the means of multiple groups and determine if the means are the same or not.


The Situation

Suppose we are interested in comparing the average miles per gallon (mpg) performance of Brand of Gas A against Brand of Gas B. Seven cars, identical in all respects except in the type of gas used, are randomly selected and placed into one of the two groups for testing (random selection helps ensure independence). Group A cars are tested with Brand of Gas A, and Group B cars are tested with Brand of Gas B. The test measurement variable is mpg. Worksheet 4.1.1 provides the mpg results.

Worksheet 4.1.1

Brand A	Brand B
20	20
20	20.5
19	18.5
16	20
15	19
17	19
14	18

Worksheet 4.1.2 provides the descriptive and inferential statistics for separately analyzing Brand A and Brand B mpg performance.

Worksheet 4.1.2

	Brand A	Brand B
Mean	17.3	19.3
Standard Error	0.9	0.3
Median	17	19
Mode	20	20
Standard Deviation	2.4	0.9
Sample Variance	5.9	0.8
Range	6	2.5
Minimum	14	18
Maximum	20	20.5
Sum	121	135
Count	7	7
Conf Level (95%)	2.2	0.8

Suppose someone told you that Brand B, with mean mpg of 19.3 is clearly a better performing gasoline than Brand A, with mean mpg of 17.3. This type of "analysis" is done everyday. You might say, "wait a minute! We have samples here and I am not so sure we can have any confidence in making statements about the populations by simply comparing the mean of one group with the mean of another group without considering sampling error. Of course, we also need to make sure that the samples were taken without bias and without measurement error - these are the non-statistical sources of error that have to be eliminated by good data collection practice.

Pause and Reflect

Recall that sampling error in learning about the true population mean from a sample of data starts with a point estimate of the population mean. The point estimate is the sample mean. Appended to that (remember the +/- of the confidence interval?) is the sampling error around the sample mean. That sampling error is a function of the standard deviation of the sample, the confidence level we wish to attain, and the sample size. So, instead of saying the population mean mpg is 17. 3 for Brand A, we say we are 95% confident that the population mean mpg is between 17.3 + 2.2 or between 15.1 and 19.5 mpg.

Likewise, we say we are 95% confident that the population mean mpg for Brand B is between is between 19.3 + 0.8 or between 18.5 and 20.1. Do you see that the two confidence intervals overlap? This means that if we took another sample of cars with Brand A gasoline, we are just as likely to get a sample mean for Brand A above 18.5. Thus, it appears that average mpg performance for Brand A and Brand B are similar, when we consider the variability around the means. Fortunately, there is a simple test in Excel for testing if two means are equal in one step. We cover that next.


Comparing Two Independent Samples of Numerical Data

The following are the null and alternative hypothesis for testing if two means are equal or not:

H₀: Mean A = Mean B
H_a: Mean A =/= Mean B

The test statistic is the t-Statistic. Its general form is:

Eq. 4.1.1: t-Stat = (Sample Mean A - Sample Mean B) - 0

Standard Error _{(Mean A - Mean B)}

Note in Eq. 4.1.1 that we are trying to determine how many standard errors the difference between two samples means is from zero. We use zero since the null hypothesis can be rewritten, Mean A - Mean B = 0. If the the null hypothesis is true, there is no difference between the means, and Mean A - Mean B would equal 0.

The formula for the standard error differs according to whether or not the population variances for the two groups are equal. If we do not have prior knowledge about that, we can get a pretty good idea by seeing if the variances of the two samples are equal or not. The test we use for comparing two variances is the F-Test. You may remember seeing the F Statistic back in regression. Do you remember the ANOVA Table? The F-Statistic compared the variability explained by regression to the variability not explained by regression (the error) - which was comparing two variances.

F Test to Compare Two Variances
The null and alternative hypotheses for comparing two variances are:

H₀: Variance A = Variance B
H_a: Variance A =/= Variance B

Excel has the F-Test as one of the Data Analysis Add-In Tools. To do the F-Test, select Tools on the Standard Toolbar, then Data Analysis in the pulldown menu, then F-Test Two Sample for Variances. In the dialog box, make Variable 1 the variable with the largest variance (Brand A in this case); and Variable 2 the variable with the smallest variance. This ensures that the F ratio will always be > 1. Select a value for alpha (such as the classic 0.05). Next, select an output range and you will get the result shown in Worksheet 4.1.3.

Worksheet 4.1.3

F-Test Two-Sample for Variances
	Brand A	Brand B
Mean	17.3	19.3
Variance	5.9	0.8
Observations	7	7
df	6	6
F	7.2
P(F<=f) one-tail	0.015
F Critical one-tail	4.3

Can you interpret the conclusion? That's right! Since two times the p-value of 0.015 is 0.030) is less than the alpha value of 0.05, reject the null hypothesis and conclude that the two variances are not equal. Side note: do you know why I doubled the p-value? Right again! The alternative hypothesis is two-tail. Excel only reports the one-tail p-value for the F-Distribution so the analyst must remember to adjust the p-value if a two-tail alternative hypothesis is being considered.

You probably had an idea we would reject the null hypothesis by seeing that the variance of A of 5.9 is quite a bit larger than the variance of the B group of 0.8. However, since the sample size is quite small, it is wise to go ahead and do the formal test.

Now that we have determined that the variances are not equal, we know which t-Test to perform.

t-Test: Two Sample Assuming Unequal Variances
We do this test with some caution. In testing for the difference between means, we assume that we are sampling from normally distributed populations with equal variances (there is an adjustment for the case in which the variances are not equal). If the populations turn out to be "not too badly skewed" (as detected through examination of the sample) and the sample size is large (30 or more in each group), the t-Test works fine. On the other hand, if the samples are small and badly skewed, it is best to do a nonparametric test, which is the subject of Module Notes 4.3.

For the purpose of demonstration, let's assume that the populations are normally distributed. We already determined that the variances are not equal. The test we want is the Two Sample t-Test assuming unequal variances. Excel has this test, which is found by selecting the Tools icon on the Standard Toolbar, then Data Analysis, then t-Test Two Sample Assuming Unequal Variances. The dialog box is similar to all of those you have seen to this point, except for the box that asks for the Hypothesized Mean Difference. The default is Zero which is what we want for testing the null hypothesis that Mean A = Mean B, or Mean A - Mean B = 0. The results are shown in Worksheet 4.1.4.

Worksheet 4.1.4

t-Test: Two-Sample Assuming Unequal Variances
	Brand A	Brand B
Mean	17.3	19.3
Variance	5.9	0.8
Observations	7	7
Hypothesized Mean Difference	0
df	8
t Stat	-2.04
P(T<=t) one-tail	0.0378
t Critical one-tail	1.860
P(T<=t) two-tail	0.076
t Critical two-tail	2.306

Let's remember what we are doing. We want to determine if average mpg for Brand A is equal to average mpg for Brand B. We do this through making an inference from our sample. We compare the sample mean of 17.3 to that of 19.3, taking into account our sampling error, and make a conclusion about the population means. We set up a two-tail hypothesis; let's use an alpha threshold of 0.05.

Since the two-tail p-value (0.076) is greater than alpha, we do not reject the null hypothesis and conclude that the means are equal - at least we do not have sufficient evidence to conclude otherwise. This means that the only reason there is a difference between the two means is due to random chance.

When this happens (failing to reject the null hypothesis), and the researcher truly believed there is a significant difference - not just random chance that the means are different - the only recourse is to go back to the test track and gather more data. So, why don't we always use samples of 30 or more? That's right: cost - it might have cost the petroleum company a lot of money to find 14 nearly identical cars.

t-Test : Two Sample Assuming Equal Variances
Now suppose we have another gasoline, Brand C, and wish to test the average mpg of seven cars running with Brand C against the average mpg performance of the seven cars with the Brand A treatment. Worksheet 4.1.5 provides the data.

Worksheet 4.1.5

Brand A	Brand C
20	20
20	26
19	23
16	24
15	23
17	25
14	23

The following are the null and alternative hypothesis for testing if these two means are equal or not:

H₀: Mean A = Mean C
H_a: Mean A =/= Mean C

I am making the assumption that the samples are drawn from normally distributed populations. This is a critical assumption since the sample size is very small. Next, we need to determine whether we use the t-Test for 2 samples assuming equal variances (in which case the variances are pooled) or the t-Test for 2 samples assuming unequal variance. To make this determination, we perform the F-Test as before.

The null and alternative hypotheses for comparing Variance A and Variance C are:

H₀: Variance A = Variance C
H_a: Variance A =/= Variance C

The results of this test are shown in Worksheet 4.1.6.

Worksheet 4.1.6

F-Test Two-Sample for Variances
	Brand A	Brand C
Mean	17.3	23.4
Variance	5.9	3.6
Observations	7	7
df	6	6
F	1.63
P(F<=f) one-tail	0.28
F Critical one-tail	4.28

Since two times the the p-value (2 * 0.28 = 0.56) is greater than alpha of 0.05, we do not reject the null hypothesis and conclude that the two variances are equal. Now we are ready to do the t-Test to determine if the two means are equal.

Worksheet 4.1.7

t-Test: Two-Sample Assuming Equal Variances
	Brand A	Brand C
Mean	17.3	23.4
Variance	5.9	3.6
Observations	7	7
Pooled Variance	4.761904762
Hypothesized Mean Difference	0
df	12
t Stat	-5.3
P(T<=t) one-tail	9.94888E-05
t Critical one-tail	1.78
P(T<=t) two-tail	0.0002
t Critical two-tail	2.18

Note from the title that this time, I selected the t-Test: Two-Sample Assuming Equal Variances when I got to the Data Analysis Add-In Tool. Since the p-value (two-tail, 0.0002) is less than 0.05, reject the null hypothesis and conclude that the two means are statistically (significantly) different. In this case, the difference we find between the two means (23.4 for Brand C vs. 17.3 for Brand A) is not a small difference due to random chance, as in our fist example, but a true difference due to a truly better performing brand of gas (Brand C).

Your colleagues in marketing are quite familiar with these kind of tests. A marketing claim that a certain product out performs another product really really needs to be backed up by an experiment with statistical conclusions.

The next module notes subject also employs a t-Test. This time, the situation involves matched pairs within the two samples rather than each sample having randomly selected observations. That will be the subject of Module Notes 4.2.3.

Before we go there, I want to show how Regression can be used for the test for differences between two means.

Regression Analysis for Determining if Two Means are Equal
You may recall the regression material concerning the categorical or dummy variable. Worksheet 4.1.8 shows how we can incorporate a dummy variable to study whether two means are equal.

Worksheet 4.1.8

Brand	MPG
1	20
1	20
1	19
1	16
1	15
1	17
1	14
0	20
0	26
0	23
0	24
0	23
0	25
0	23

Here I used the dummy variable to identify which brand of gas the cars received. A "1" represents Brand A, a "0" represents Brand C. Thus, brand of gas is the independent variable and mpg is the response dependent variable. Worksheet 4.1.9 provides the regression analysis.

Worksheet 4.1.9

SUMMARY OUTPUT
Regression Statistics
Multiple R	0.835463491
R Square	0.697999245
Adjusted R Square	0.672832515
Standard Error	2.182178902
Observations	14
ANOVA
	df	SS	MS	F	Significance F
Regression	1	132.0714286	132.0714286	27.735	0.0002
Residual	12	57.14285714	4.761904762
Total	13	189.2142857
	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	23.42857143	0.824786099	28.40563324	2.24814E-12	21.63151693	25.22562593
Brand	-6.142857143	1.166423687	-5.266402947	0.0002	-8.684275994	-3.601438292

The regression equation is:

Eq. 4.1.2. E(MPG) = 23.4 - 6.1(Brand).

For Brand A = 1, E(MPG) = 23.4 - 6.1 = 17.3
For Brand C = 0, E(MPG) = 23.4

Note that regression gave us the same results as the t-Test! The averages for Brand A and Brand C came out identical to those reported in Worksheet 4.1.9. Also note that the p-value for testing the significance of the regression is identical to the p-value for testing if the means are different (0.0002). The reason the tests are identical is that the slope in the regression equation for the dummy variable is simply the difference between the average value of Y when X = 1 (Brand A), and the average value of Y when X = 0 (Brand C). So we are simply comparing the average mpg of Brand A cars against Brand C cars, and the conclusion would be that the means are significantly different (in the regression sense, the qualitative or dummy variable is important).

The line fit plot visibly shows the significant difference between the means.

Worksheet 4.1.10




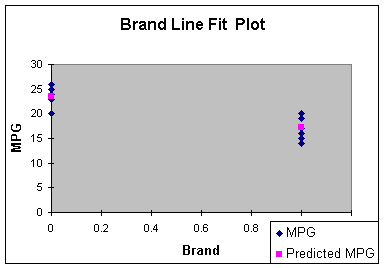
Reference:


Anderson, D., Sweeney, D., & Williams, T. (2001). Contemporary Business Statistics with Microsoft Excel. Cincinnati, OH: South-Western, Chapter 10 (Sections 10.1 and 10.2).