|
Main
Module 3 |
|
Learning Objectives |
|
At the end of the module, the student will:
∑ the relationship between a dependent variable and multiple independent quantitative variables; and use relationship for prediction. ∑ the relationship between a dependent variable and qualitative independent variables; and use the relationship for prediction. ∑ interaction; and use interaction models for prediction.
|
|
The following sub modules contain summary notes for the three content topic areas of Module 3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Assignment 3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Part A: Select a realistic and interesting data set consisting of a sample of approximately 50 observations (n = 50). Your data set should include a quantitative dependent variable (Y), and two independent (X - predictor) variables, one quantitative (QN) and one qualitative (QL). Example: Y
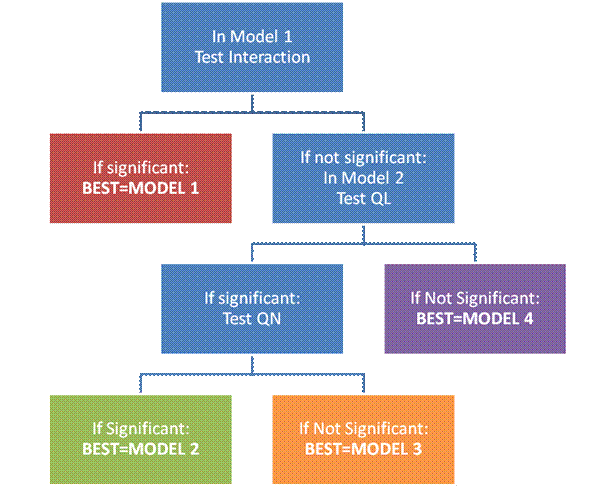
= Salary of USF Professor Please select a qualitative variable with exactly two-levels (male/female; in-season/off-season; large cap fund/small cap fund). Also, try to select about the same number of data points for each level, for example, 25 males and 25 females. 1. In an Excel Spreadsheet, enter the QN data in a column, enter the QL data in a column, create a column for QN*QL interaction (where "*" indicates multiple respective QN data times QL data, and enter Y data in a column. Note: all independent variables should be contiguous or adjacent to each other). 2. Using the data analysis tool, build and test at least two of the following models, in the process of determining your "best" model. For each test, be able to state the null and alternate hypotheses, the hypothesized regression equation associated with the null and alternate hypotheses, the appropriate p-value, the null hypothesis decision (reject or do not reject the null hypothesis), and the resulting conclusion (e.g., curvature is important, interaction is not important or not significant). A flowchart to guide model testing is provided in Item 4. Model 1: E(Y) = B0 + B1 QN + B2 QL + B3 QN*QL Model 2: E(Y) = B0 + B1 QN + B2 QL Model 3: E(Y) = B0 + B2 QL Model 4: E(Y) = B0 + B1 QN 3. Using the data analysis regression
tool, build Model 1. 4. Follow the decision model to build
the best model.
5. Rerun the data analysis regression tool for your "best" model, and include and be able to describe or interpret the following printouts:
6. Be able to demonstrate your
knowledge of the learning objectives as applied to this Assignment in Exam 3. Part
B: Application
problems (show your work where required for full points) 1. The following regression model has been
proposed to predict sales at a fast food outlet. E(Y)† = 18 - 2X1 + 7X2 + 15X3†† where ††††††††††† X1 = the number of competitors within 1 mile ††††††††††† X2 = the population within 1 mile (in 1,000s) ††††††††††† X3 = 1 if drive-up windows are present, 0 otherwise ††††††††††† † E(Y) = sales (in
$1,000s) ††††††††††† a.†††††††† What is
the interpretation of 15 (the coefficient of X3) in the regression equation? ††††††††††† b.†††††††† Predict
sales for a store with 2 competitors, a population of 10,000 within one mile,
and one drive-up window (give the answer in dollars). ††††††††††† c.†††††††† Predict
sales for the store with 2 competitors, a population of 10,000 within one
mile, and no drive-up window (give the answer in dollars). 2. A company has recorded data on the
weekly sales for its product (y),
the unit price of the competitorís product (x1), and advertising expenditures (x2).† The data resulting from a random sample of
7 weeks follows.† Use Excelís
Regression Tool to answer the following questions (attach output for
inspection).
a.†††††††† What is the estimated regression
equation? ††††††††††† b.†††††††† Determine
whether the model is statistically significant overall.† Use a = 0.10. ††††††††††† c.†††††††† Determine
if price is significantly related to sales.†
Use a =
0.10. ††††††††††† d.†††††††† Determine
if advertising is significantly related to sales.† Use a = 0.10. ††††††††††† e.†††††††† Find
and interpret the practical utility of the model. 3. The following regression
model has been proposed to predict monthly sales at a shoe store. E(Y)† = 40 - 3X1 + 12X2 + 10X3†† where ††††††††††† X1 = competitor's previous month's sales (in $1,000s) ††††††††††† X2 = Stores previous month's sales (in $1,000s) †††††††††† †X3 = 1 if radio advertising is used; X3= 0
otherwise ††††††††††† E(Y) = sales (in $1000s) ††††††††††† a.†††††††† Predict
sales (in dollars) for the shoe store if the competitor's previous month's
sales were $9,000, the store's previous month's sales were $30,000, and no
radio advertisements were run. ††††††††††† b.†††††††† Predict
sales (in dollars) for the shoe store if the competitor's previous month's
sales were $9,000, the store's previous month's sales were $30,000, and 10
radio advertisements were run. 4. The following estimated
regression model was developed relating yearly income (Y in $1,000s) of 30
individuals with their age (X1) and their gender (X2); (X2=0 if male and X2=1
if female). E(Y)† = 30 + 0.7X1 + 3X2 4.1†††††† From the above function, it can be said that the expected
yearly income of ††††††††††† a.†††††††† males
is $3 more than females ††††††††††† b.†††††††† females
is $3 more than males ††††††††††† c.†††††††† males
is $3,000 more than females ††††††††††† d.†††††††† females
is $3,000 more than males 4.2.††††† The yearly income of a 24-year-old female individual is ††††††††††† a.†††††††† $19.80 ††††††††††† b.†††††††† $19,800 ††††††††††† c.†††††††† $49.80 ††††††††††† d.†††††††† $49,800 5. A regression model between
sales (Y in $1,000), unit price (X1 in dollars) and television advertisement
(X2 in dollars) resulted in the following function: E(Y) = 7 - 3X1 + 5X2 5.1 The coefficient of the
unit price indicates that if the unit price is ††††††††††† a.†††††††† increased
by $1 (holding advertising constant), sales are expected to increase by $3 ††††††††††† b.†††††††† decreased
by $1 (holding advertising constant), sales are expected to decrease by $3 ††††††††††† c.†††††††† increased
by $1 (holding advertising constant), sales are expected to increase by
$4,000 ††††††††††† d.†††††††† increased
by $1 (holding advertising constant), sales are expected to decrease by
$3,000 5.2 The coefficient of X2
indicates that if television advertising is increased by $1 (holding the unit
price constant), sales are expected to ††††††††††† a.†††††††† increase
by $5 ††††††††††† b.†††††††† increase
by $12,000 ††††††††††† c.†††††††† increase
by $5,000 ††††††††††† d.†††††††† decrease
by $2,000 For the next 4 questions,
refer to printout A1 found at the end of this assignment. Use alpha level of
0.01 6.† Write the least squares regression equation
(use words for Y, QN and QL, and numbers for Bís). 7.† How much of the variation in the heating
cost is explained by the variables in the final model? Report the statistic
you inspected to obtain your answer. 8. Are all the regression
coefficients in the model significant? Indicate which ones (if any) and
justify your answer with the appropriate statistic (remember that alpha level
is 0.01) 9. Explain the
numerical/practical meaning of the regression coefficient for the Garage
variable. Printout A1 A federal agency is interested
in studying the impact of several variables (mean outside air temperature,
thickness of attic insulation, attached garage) in the cost of heating a
home. The agency commissioned a company to survey several houses in a
particular region and arrived at the following regression output:
10. The Director of
Undergraduate Studies at the School of Business wanted to investigate two
important questions: How important is GPA in determining the starting salary
of recent business school graduates, and if graduating from a business school
increases the starting salary.† She
gathered the following sample information on 15 graduates last fall to
investigate these questions.† The result
is shown in Table 1. TABLE 1††††††† †††††††††† †
In the study, the Salary is
reported in $000, GPA on the traditional 4-point scale, and Business status
is coded as 1 if a student graduated from a college of business, and 0 if
from another school. Answer the following questions (attach Excel output for
inspection). a) Determine the estimated
regression equation b) How much does graduating
from a college of business add to a starting salary? c) Discuss the practical
utility of the model. d) Discuss the model's
statistical significance (you assign a value for the alpha) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
-x-x-x- Practice
problems (not for grading) Solve
multiple linear regression applications through this link Optional Text Reading (Additional resources) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Anderson, D., Sweeney, D.,
& Williams, T. (2007). Essential of Modern Business Statistics with
Microsoft Excel. Cincinnati, OH: South-Western. Chapter 13. Ken
Black. Business Statistics for Contemporary Decision Making. Fourth
Edition, Wiley. Chapter 13, 14 & 15 D. Groebner, P. Shannon, P. Fry & K. Smith.† Business Statistics: A Decision Making Approach, Fifth Edition, Prentice Hall, Chapter 12 & 13 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||