|
Index to Module Three Notes
|
Multiple regression and
correlation analysis is similar to simple linear regression and correlation in
that it involves the study of the form, direction and strength of
relationships. But with multiple regression, the relationship is between the
dependent variable (Y) and multiple independent variables X1, X2,
X3,… Xn, that help us to better explain or predict the
dependent variable (Y). The analysis is
similar to simple linear regression but adding new variables lead to additional
considerations as well. The general multiple regression equation with n independent variables is given by:
E(Y)
= B0 + B1 X1 + B2X2 + B3
X3 + …+ Bn Xn where:
B0
is the intercept, the value of Y when all X's are zero
Bi is the amount by which Y changes when a particular Xi increases by one unit with all other values held constant. The subscript i can assume values between 1 and n, which is the number of independent variables
For example, we could
hypothesize that the fuel efficiency of a vehicle (variable Y) as measured by
miles per gallon (MPG) is related to the octane rating of the gasoline being
used (X1) and to its horsepower (X2). Therefore we can write a general multiple
regression equation relating the independent variables with the dependent
variable as:
E(Y) = B0 + B1 X1
+ B2 X2 ….or:
E(MPG) = B0 + B1
(Octane) + B2 (HorsePower)
We could also hypothesize
that curb weight is related to the vehicle's performance and we may want to
include this additional independent variable (X3) in the multiple
regression equation:
E(Y) = B0 + B1 X1
+ B2 X2 + B3 X3….or:
E(MPG) = B0 + B1
(Octane) + B2 (HorsePower) + B3 (CurbWeight)
As in Module 2, we will use
the seven steps to estimate regression parameters, test the practical and
statistical utility of the estimated model, evaluate assumptions and use the
model for prediction. The values for the coefficients in the multiple
regression equation are found by using the least squares method. Recall that this method makes the sum of the
squared differences between the predicted and the actual values of Y as small
as possible. Because the computations
are intensive, we'll rely on Excel to generate the b0, b1,
b2, and b3 - which will be used as the estimates of
regression parameters B0, B1, B2, and B3;
statistical tests, and related measures of model's adequacy.
The seven steps we used to
study simple linear regression in Module 2 will be applied for multiple
regression as well. They are repeated here for convenience with a particular
form of a model which will be reviewed in this module 3:
1. Hypothesize regression model
E(Y) = B0 + B1 X1 + B2X2 + B3 X1 X2
2. Gather data and examine
relationships with graphs (scatter diagrams)
3. Estimate regression model parameters
4. Test practical utility of regression model
5. Test statistical utility of regression model and multiple independent terms
6. Evaluation assumptions of regression model
7. Use model for prediction
Note that the first step shows the addition of another independent variable, X2.
That variable could be another numerical variable or a categorical variable
used to stratify the data. Examples of categorical or qualitative variables
include male/female, in-season/out of season, and defective/not defective. The
final term that has been added is a mathematical way of capturing a concept
called interaction. Interaction allows us to model situations where the
relationship between Y and X1 is said to depend on X2.
The objective of Module 3 is to introduce model building skills that will
enable you to model relationships involving multiple numerical and categorical
variables. Module 3.2 Notes will cover incorporating categorical variables and
interaction separately. Model 3.3 Notes will cover model-building skills that
will hopefully put everything together.
The purpose of Module 3.1 Notes is to introduce multiple regression by the
addition of just one more numerical independent variable. Module Notes 3.1, 3.2
and 3.3 are designed to prepare you for Assignment 3. These note sets relate to
optional readings in Chapter 13 of the Anderson, Sweeney & Williams
reference given at the end of the note sets.
Let's go through the 7 steps applied to multiple regression with the
following example where we added a second independent variable representing the
experience of the auditor as measured by his/her years of experience. In general, we add variable in a model to increase
its explanatory power as measure by R2. If you recall, R2 in Module 2 is
0.82, meaning that approximately 82% of the sample variation in variable
ExtHours is explained by variable Assets.
Step
1: Hypothesize the regression model
Equation 3.1.1 illustrates
a model similar to that used in Module 2; a model to predict the external hours
of time needed to audit a client based on client assets and the years of
experience of the audit leader (abbreviated Exp in this illustration). My idea,
or hypothesis, is that as client assets increase, external hours increase at a
constant rate (positive linear relationship); and as the years of experience of
the audit leader increase, external hours decrease at a constant rate (negative
linear relationship).
Eq. 3.1.1: E(Y) = B0 + B1X1 - B2X2; or
E(ExtHours) = B0 + B1(Assets) - B2(Exp)
Caution
When we add a second
(or many) independent numerical variable(s), we want to add independent variables that correlate strongly
with the dependent variable, but weakly with the other independent
variables already in the model. As a rule of thumb, I like to make sure the
correlation coefficient between any of the pairs of independent variables is
less than +0.7 and greater than -0.7. If two or more independent variables are
strongly related to each other, we get what's called multicollinearity.
This condition makes it difficult to determine the contribution of the
individual independent variables, and also adversely affects model
interpretation.
Step 2:
Gather Data
When you are
exploring whether or not independent variables will contribute to effective
predictive models, you may wish to run separate scatter diagrams between Y and
each of the independent variables, and determine the correlation between Y and
each of the independent variables. Here is the data I have selected for this
example. Assets are in $000s, as in Module 2; Exp (Experience of the audit team
leader) is in years; and ExtHours (external hours to perform the audit) are in
hours. Assets and Experience are the independent variables being used to
predict External Hours, the dependent variable.
Worksheet 3.1.1
|
Assets |
Exp |
ExtHours |
|
3200 |
8 |
700 |
|
3000 |
7 |
900 |
|
3500 |
9 |
800 |
|
4000 |
6 |
900 |
|
4700 |
8 |
880 |
|
5000 |
6 |
850 |
|
6000 |
5 |
1000 |
|
5500 |
6 |
1000 |
|
6500 |
7 |
950 |
|
6500 |
4 |
1100 |
|
7000 |
5 |
1200 |
|
4500 |
9 |
830 |
|
7500 |
3 |
1100 |
|
5750 |
6 |
1100 |
|
7250 |
5 |
1160 |
|
8000 |
8 |
1120 |
|
8000 |
4 |
1300 |
|
8500 |
4 |
1400 |
|
9000 |
7 |
1500 |
|
8500 |
2 |
1200 |
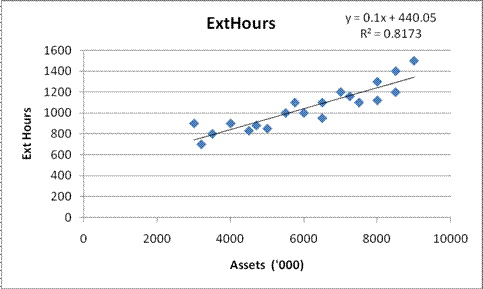
Next, I ran the scatter
diagrams relating External Hours to Assets (Worksheet 3.1.2), and External
Hours to Experience (Worksheet 3.1.3).
Worksheet 3.1.2
Worksheet 3.1.3
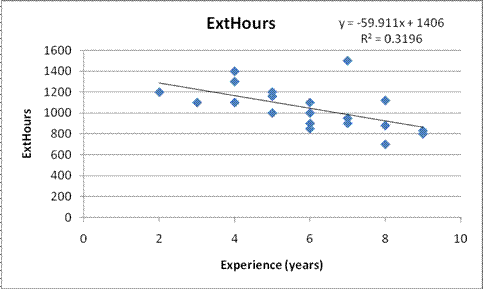
Worksheet 3.1.2 shows the moderately strong positive linear relationship
between External Hours and Assets. Worksheet 3.1.3 does show a negative linear
relationship, but not as strong as we would like. Remember that we use the
correlation coefficient, r, to measure strength of the linear relationship
between two variables. While we can take the square root of the coefficients of
determination, there is an Excel Data Analysis Add-In that lets us create all
of the pair-wise correlation coefficients at once. Worksheet 3.3.4 shows the
result. To get the correlation matrix, select Tools from the Standard
Toolbar, Data Analysis from the pulldown menu, Correlation, (in Excel 2007,
select Data tab, then Data Analysis option, then Correlation from the dialogue
box), then respond to the dialog box entry questions. If the data in
Worksheet 3.1.1 above started in Column A, Row 1, and extended through Column
C, Row 21, the input range for the first dialog box is A1:C21. I remember to
check the Labels circle, then place the output near my data, such as D1. Click OK
and Worksheet 3.1.4 shows the results:
Worksheet 3.1.4
|
Assets |
Exp |
ExtHours |
|
|
Assets |
1 |
||
|
Exp |
-0.605951 |
1 |
|
|
ExtHours |
0.90407 |
-0.565325 |
1 |
Note the less than moderate relationship between the two independent variables,
Assets and Experience (-0.606): that's good. But also note the fairly weak
relationship between the dependent variable, External Hours, and
Experience (-0.565): that's not so good if we want to improve our prediction of
External Hours.
Model builders like to use the principle of parsimony or keeping models
as simple as possible (I've heard this called kis - keep it simple, but
prefer the more academic term!). When we build multiple regression models, we
do run the risk of making something too complicated to interpret and
understand, especially when the addition of a variable does not contribute to
the prediction of the dependent variable. I want to continue with the addition
of a fairly weak variable to illustrate this point.
Pause
and Reflect
We are introducing a
subject that involves building bigger models than the simple linear regression
model. However, we need to be careful that we use good science in building
these bigger models. Just because a model is bigger doesn't make it better -
sometimes it's just bigger.
Step
3: Estimate the Regression Parameters
To estimate the regression
parameters and generate all of the regression statistics and graphs, use the
Regression Data Analysis Add In as we did in Module 2. Select Tools from
the Standard Toolbar, Data Analysis from the pulldown menu,
Regression, and then respond to the dialog questions as you did in building
a simple linear regression model. The difference is that the X range will
include highlighting all of the columns containing the X variables rather than
just one column. Caution: when you load data, be sure to put all of the
X variables in contiguous columns to allow their selection at one time (Note
Worksheet 3.1.1 shows the two independent variables in adjacent columns).
Worksheet 3.1.5 illustrates the Regression Summary.
Worksheet 3.1.5
|
SUMMARY OUTPUT |
||||||
|
Regression Statistics |
||||||
|
Multiple R |
0.9043379 |
|||||
|
R Square |
0.8178270 |
|||||
|
Adjusted R Square |
0.7963949 |
|||||
|
Standard Error |
93.699570 |
|||||
|
Observations |
20 |
|||||
|
ANOVA |
||||||
|
Df |
SS |
MS |
F |
Significance F |
||
|
Regression |
2 |
670041.6392 |
335020.8196 |
38.15897 |
5.18E-07 |
|
|
Residual |
17 |
149253.3608 |
8779.609459 |
|||
|
Total |
19 |
819295 |
||||
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
|
Intercept |
468.78422 |
153.59229 |
3.0521337 |
0.007206 |
144.7324 |
792.8361 |
|
Assets |
0.0981388 |
0.0143926 |
6.8186667 |
2.99E-06 |
0.067773 |
0.128505 |
|
Exp |
-2.931174 |
13.790612 |
-0.2125485 |
0.834207 |
-32.02687 |
26.16452 |
|
RESIDUAL OUTPUT |
PROBABILITY OUTPUT |
|||||
|
Observation |
Predicted ExtHours |
Residuals |
Standard Residuals |
Percentile |
ExtHours |
|
|
1 |
759.3791346 |
-59.379134 |
-0.6699595 |
2.5 |
700 |
|
|
2 |
742.6825406 |
157.31745 |
1.7749726 |
7.5 |
800 |
|
|
3 |
785.8896132 |
14.1103868 |
0.1592038 |
12.5 |
830 |
|
|
4 |
843.7525607 |
56.247439 |
0.6346254 |
17.5 |
850 |
|
|
5 |
906.5874023 |
-26.587402 |
-0.2999788 |
22.5 |
880 |
|
|
6 |
941.8914058 |
-91.891405 |
-1.0367872 |
27.5 |
900 |
|
|
7 |
1042.961426 |
-42.961425 |
-0.4847227 |
32.5 |
900 |
|
|
8 |
990.9608284 |
9.0391716 |
0.1019866 |
37.5 |
950 |
|
|
9 |
1086.168499 |
-136.16849 |
-1.5363543 |
42.5 |
1000 |
|
|
10 |
1094.962023 |
5.0379765 |
0.0568422 |
47.5 |
1000 |
|
|
11 |
1141.100271 |
58.899728 |
0.6645505 |
52.5 |
1100 |
|
|
12 |
884.0284583 |
-54.028454 |
-0.6095892 |
57.5 |
1100 |
|
|
13 |
1196.032044 |
-96.032043 |
-1.0835048 |
62.5 |
1100 |
|
|
14 |
1015.49554 |
84.504462 |
0.9534422 |
67.5 |
1120 |
|
|
15 |
1165.634982 |
-5.6349823 |
-0.0635780 |
72.5 |
1160 |
|
|
16 |
1230.445591 |
-110.44559 |
-1.2461293 |
77.5 |
1200 |
|
|
17 |
1242.170291 |
57.829708 |
0.6524778 |
82.5 |
1200 |
|
|
18 |
1291.239714 |
108.76028 |
1.2271144 |
87.5 |
1300 |
|
|
19 |
1331.515611 |
168.48438 |
1.9009662 |
92.5 |
1400 |
|
|
20 |
1297.102064 |
-97.10206 |
-1.0955777 |
97.5 |
1500 |
|
Look in the intercept,
Assets and Experience Rows, in the Coefficients Column, to obtain the
regression coefficients. These are repeated in Equation 3.1.2.
Eq. 3.1.2: ExtHours = 468.8 + 0.10 (Assets) - 2.9 (Experience)
The intercept, 468.8, is interpreted as in simple linear regression. External
hours equal 468.8 when assets and experience equal to zero. Since we did not
have any observations where assets and experience equal zero, there would be no
practical interpretation.
The slope of 0.10 for assets means that external hours increase by 0.10 when
assets increase by one ($1,000 since assets are in $000s), holding experience
constant (that is, for interpretations involving team leaders with similar
experience). The slope of -2.9 means that external hours decrease by 2.9 when
experience increases by 1 year, holding assets constant (at similar levels).
Step
4: Test Practical Utility of Regression Model
As with simple linear
regression, we use R2 and Standard Error of the Model to test
practical utility of the model.
Coefficient of Multiple Determination, Adjusted R2
The R2 in multiple regression is called the coefficient of
multiple determination. It is safest to use the Adjusted R2 (called
Adjusted R Square in Excel), as this statistic adjusts for the number of
independent variables in relation to sample size to prevent overestimating the
amount of variability explained by the independent variables. A rule of thumb
in multiple regression is that we should have at least 10 observations for each
regression parameter. This model has three regression parameters (the intercept
B0 and the two slopes, B1 and B2) so we should
have 30 observations. We only have 20 so the adjusted R2 is a bit
lower than the R2 - sort of like keeping us honest. The formula used
by Excel to compute the adjusted R2 is:
Eq. 3.1.3: R2adjusted = 1 - { ( 1 - R2) * [ (n - 1) / (n - 2) ] }
From this formula, you can
see that if the sample size was 1,000, the difference between adjusted R Square
and R Square is negligible.
The adjusted R Square is found in the Regression Statistics near the top of
Worksheet 3.1.5. It is 0.796. The interpretation: assets and experience explain
79.6% of the sample variation in external hours. As in simple linear
regression, we would like this to be as close to 100% as possible. A rule of
thumb benchmark might be at least above 50%. If you are comparing two models,
the model that is most practically useful, if everything else is equal, is the
model with the highest adjusted R2.
Standard Error of the Model
The Standard Error of the Model or Estimate is found directly below the
adjusted R2. It is 93.7. The interpretation: we would expect 95% (or
most) of the actual values of external hours to be within +/- 2 * 93.7 of the
predicted external hours. As with simple linear regression, we want the
standard error to be as low as possible. A benchmark might be the standard
error (93.7) divided by an actual values of Y (external hours) should be lower
than ranges between .05 and 0.15, or 5% to 15%. If you are given two models,
the model with the lowest standard error, if everything else is equal, is the
model with the most practical utility.
Pause
and Reflect
Although testing
practical utility involves benchmarks and judgment, it is very important.
Models that are not judged practically useful should not be used, even if they
are proven to be statistically significant or useful. A model could have a very
steep slope and thus be statistically significant, but it might have too much
error around the regression line to be of practical use.
Step
5: Test Statistical Utility
There are multiple
hypothesis tests in multiple regression because not only can we test for
statistical utility of the model, but we can also test for statistical utility of
the multiple independent variables.
Is the Model Statistically
Significant or Useful?
The null and
alternative hypotheses to test for model statistical utility are:
H0:
B1 = B2 = 0 (the model is not statistically useful)
Ha: At least 1 B is =/= 0 (the model is statistically useful)
(remember, =/= is the closest I can come to the "not equal" symbol)
The test statistic for this test of hypothesis is the F, which has a value of 38.16 (look in the Regression row of the ANOVA table in Worksheet 3.1.5, under the F Column). Recall, in concept, the F measures the ratio of variation explained by the regression model to the variation unexplained. The farther this number is from 1, the more variation is explained related to unexplained. The p-value for the F is 5.28E-07, or 0.000000528 (look in the Regression row of the ANOVA table in Worksheet 3.1.5,under the Significance F column). Since the p-value of 5.28E-07 is less than an alpha of 0.01, we reject the null hypothesis and conclude the model is statistically useful.
Attention
to Detail
Did you notice that I
used an alpha of 0.01, whereas I have been using convention of an alpha of 0.05
before now? We are entering into a new hypothesis test procedure in multiple regression
where we do multiple hypothesis tests on the same data (with this example, we
could actually do three tests: a model test, a test on X1, and a
test on X2). Each test with the same data theoretically increases
the error of rejecting a true null hypothesis. So, research convention suggests
that we lower the alpha to 0.01 when we do multiple tests with the same data.
Are Assets Statistically
Significant or Useful?
We can also test for
statistical significance of the individual independent variables. The null and
alternative hypotheses to test for the importance of assets are:
H0:
B1 = 0 (assets are not important or not statistically useful)
Ha: B1 =/= 0 (assets are important or statistically
useful)
The test statistic is the t,
which has a value of 6.82. This is found in the Asset row of the regression
statistics in Worksheet 3.1.5. It's value implies that the slope of 0.098 or
0.10 is 6.82 standard errors of the slope from zero. The associated p-value is
2.99E-06. Since the p-value is less than an alpha value of 0.01, reject the
null hypothesis and conclude that assets are important in predicting the value
of external hours.
Is Experience Statistically Significant or Useful?
We can similarly test for the statistical significance of the experience
variable.
H0:
B2 = 0 (experience is not important or not statistically useful)
Ha: B2 =/= 0 (experience is important or statistically
useful)
The t statistic for this test is found in the Experience row of the regression summary. Its value is -0.21, with an associated p-value of 0.834. Since the p-value is greater than an alpha of 0.01, we fail to reject the null hypothesis and conclude that experience is not useful in predicting external hours. We added a variable that has no statistical utility and it should be removed from the model, at least in its current form. Another variable might be considered, or the analyst may just decide to go with assets for predicting external hours.
Caution
When I say that
Experience is not of statistical utility or important in helping to predict
External Hours, we must realize that we are only testing experience in it's linear
form at this point.
There may be a slight
chance that experience is important in a curvilinear relationship with external
hours. We will talk more on this in Module 3.2 Notes.
A last point before we go on
to Step 6. Note in the Experience row of Worksheet 3.1.5 that the Lower 95% and
Upper 95% Confidence Levels are -32.03 and 26.16 for the slope coefficient of
-2.93. The interpretation: we are 95% confident that when experience increases
by 1 year, the change in predicted external hours is between a decrease of 32
hours and an increase of 26 hours. Since sometimes external hours decrease, and
sometimes external hours increase when experience increases by one, knowledge
of experience does not help in predicting external hours. The 95% confidence
interval on the slope confirms why we did not reject the null hypothesis of no
statistical relationship between experience and external hours.
Step
6: Evaluate Assumptions of Regression Model
The assumptions and their evaluation are the same as in simple linear
regression. The error or residual term should be normally distributed with mean
of zero; the error should be constant for all values of the independent variables;
and the error should be independent.
We evaluate the first assumption by examining the standardized residuals to see
if any error terms are more than three standard errors from the regression
line. The normal probability plot can also be used. The idea is that this
assumption is generally met unless there are extreme values that would cause a
skew in the data. In the Residual Output section of Worksheet 3.1.5, in the
column "Standard Residuals," we find no value greater than +3 or less
than -3. Thus, we would declare that this assumption is met.
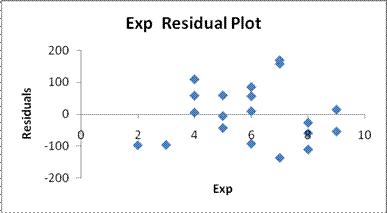
The second and third assumptions are evaluated by looking at the residual
plots. Worksheet 3.1.6 illustrates one of the two residual plots (one residual
plot for each independent variable will be automatically produced by the
regression add-in to Excel). This plot shows that the error terms do not
exhibit a distinct pattern and are fairly constant in their departure from zero
for the various values of the independent variable. Both residual plots would
have to be so evaluated. As long as there is fairly constant departure from
zero for all values of the independent variable, and as long as there is no
distinct pattern such as a cone or football or curve, the second and third
assumptions are met.
Worksheet 3.1.6
Step 7: Use Model for Prediction
If the multiple
regression model proves to be statistically and practically useful, and if the
assumptions are met, it can then be used for prediction with confidence. I
recognize that this model had a problem in that the second independent
variable, experience, was determined to be of no statistical utility. The
analyst would be better off building a new model without the experience
variable, perhaps using some other variable or simply use assets as the single
independent variable.
However, I would like to go ahead and make a prediction just to demonstrate the
step. As with simple linear regression, we begin by making a point estimate
prediction. Let's make our prediction for the first observation in the data
set. This prediction involves values of the independent variables as follows.
The value for assets is $3,200,000 and the value for audit team leader
experience is 8 years. The point estimate is then:
Eq. 3.1.4: ExtHours = 468.8 + 0.10 (3200) - 2.9 (8) = 765.6
The second step is to make the prediction interval for this observation. We are 95% confident that for a client with $3,200,000 in assets, and with an audit team leader having 8 years of experience, the audit will take:
Eq. 3.1.5: ExtHours = 765.6 + 2 * standard error of model
ExtHours = 765.6 + 2 * (93.7)
ExtHours = 765.6 + 187.4 or 578.2 to 953.
As a closing note, the actual audit took 700 External Hours for the first observation,
which gives an error of -65.6. That error is 9.4% of the actual value.
Excel will produce line fit plots showing the predicted values of Y for all the
values of X1 and X2, but produces these as separate
two-dimensional plots. It does not have the capability to illustrate the
multidimensional surface represented by the multiple regression prediction
model.
That ends the introduction. Next, we examine how to incorporate categorical
variables and interaction into the multiple regression model.
Reference:
Anderson, D., Sweeney, D., & Williams, T. (2007). Essentials of Modern Business Statistics with Microsoft Excel. Cincinnati, OH: South-Western, Chapter 13.
D. Groebner, P. Shannon, P.
Fry & K. Smith. Business Statistics:
A Decision Making Approach, Seventh Edition, Prentice Hall, Chapter 15.
Ken
Black. Business Statistics for Contemporary Decision Making. Fourth Edition,
Wiley. Chapter 13 & 14
| Return to Module Overview | Return to top of page |