|
Module
1.3 Notes |
|
Index to Module One Notes
|
Measures
of Central Tendency
In describing a set
of data, we are interested in the numerical measures of center and spread.
Recall in the cycle time example of Module 1.2, the center of the data appears
to be a cycle time of 21 days. That is formally called the measure of
central tendency of the data. There are two classic ways to measure the
center of a distribution of data: the mean and the median.
Mean
The mean or average is the arithmetic measure of central tendency,
and is simply the sum of all of the observations in a set of data divided by
the total number of observations. So, the mean of seven cycle times with values
21, 23, 19, 22, 20, 22, 20 is:
Mean = (21 + 23 + 19 + 22 + 20 + 22 + 20) / 7 = 21
You will read in statistics
texts that this is the formula for both the population mean (its symbol is the
Greek letter mu) and the sample mean (its symbol is an x with a bar over it, or
x-bar). Don't get alarmed - this is not a course with a lot of formulas,
symbols and computations - we will let the computer do it. I just want to
highlight the computations for the classic measures in descriptive statistics.
You will also read in textbooks that measures based on a population are called parameters,
and measures based on a sample are called statistics.
Median
The median is called the location measure of central tendency since
it is the middle value of an ordered array of observations - 50% of the
observations in a set of data fall below the median provided the data is in an
ordered array. Since we have to account for 100% of the data, 50% of the
observations fall above the median. So, given the cycle times of 21, 23, 19,
22, 20, 22, 20; first created an ordered array (sorted list of the numbers):
Ordered array = 19, 20, 20 , 21, 22, 22, 23
The median is the ordered or ranked observation that appears at location = (n + 1)/2, where n is the symbol for the number of numbers in the set of data. For this ordered array:
Median = (7 + 1) / 2 = 4th ordered observation, which is the number 21.
Do you note that the mean and the median are equal? They will be approximately equal (such as within 5% of each other) as long as the distribution of the set of data is somewhat symmetric without extreme values (signals or outliers) to one side or the other. This is an important point. Suppose we had an outlier or signal cycle time of 38 instead of 23. Let's calculate the mean and the median:
Mean = (19, 20, 20, 21, 22, 22, 38) / 7 = 23.14
Median = (7 + 1) / 2 = 4th ordered observation, which is 21
The mean was
"pulled" to the outlier value of 38 - the mean is not resistant to
extreme values, but the median is since it is a location and not arithmetic
measure. Note that the mean is about 10% greater than the median: 21 is more
representative of the center when the distribution is not symmetric. As an
aside, economists generally use the median when reporting the measure of center
for housing values since sets of housing data are often skewed by high or low
extreme values. It would be misleading or even unethical to report the mean
housing value as a measure of center when there are extreme values on the high
side - the median is more representative of center in that case. Also note that
when the mean > median, the distribution is skewed right - you saw a
histogram picture of that in Worksheet 1.2.3 of Module 1.2. Similarly, when the
mean < median, the distribution would be skewed left - you saw a
histogram picture of that in Worksheet 1.2.4 of Module 1.2.
Before we go on, let me show you how to compute the median with an even set of
data. Suppose we have the numbers 19, 20, 20, 21, 22, 22, 23, and 23. The
median is:
Median = (n + 1) / 2 = (8 + 1) / 2 = 4.5th ordered observation; the number at the 4.5th location is the average between the 4th and 5th numbers or 21.5
Mode
Sometimes you hear of the mode as a measure of central tendency.
However, the mode is simply the most frequently appearing number in a data set,
so there are actually two modes in the above distribution, 20 and 22. We will
not be using the mode as a measure of central tendency, but only to help in
general examination of shape, as discussed in Module 1.2.
Pause and Reflect
The mean and the median are measures of center. The mean and median will be approximately equal for symmetric sets of data. The median is resistant to extreme values, whereas the mean is pulled towards them. When the mean > median, the distribution is skewed right by an extreme value(s) > mean. When the mean < median, the distribution is skewed left by an extreme value(s) < mean. Thus, for sets of data with extreme values, the median is more representative of the center, and is the preferred measure. Alternatively, the extreme values could be removed from the data for separate study, and a new, more accurate arithmetic mean can then be computed.
Measures
of
Equally important to
describing the center of a set of data with a numerical measure, is describing
the spread or variation in a set of data. There are three classic ways to
measure variation. The simplest measure of spread is the range. In the
data set, 19, 20, 20, 21, 22, 22, 23:
Range = Maximum Number - Minimum Number = 23 - 19 = 4
So there is a spread of four
days between the smallest and largest cycle times.
Standard Deviation
The range is not very rich - it ignores all but two numbers. If the
distribution is approximately normal or a symmetric bell-shape, the classic
measure of variation is the standard deviation. To set the stage for the
standard deviation, recall that the mean of these numbers is 21. The number 19
varies from 21 by - 2, the number 20 varies by -1, the number 23 by +2, and so
forth. The standard deviation is simply a measure of the average of these
deviations. To compute the standard deviation for a population of numbers 19,
20, 20, 21, 22, 22, 23; first find the mean (we already did that, it is 21).
Now subtract each number from the mean, square the result (to get rid of
plusses and minuses), sum the resulting squared deviations, and divide by the
number of numbers. This is called the variance of the population. The standard
deviation of the population (the symbol is the Greek letter sigma) is the
square root of the variance:
Mean = (19 + 20 + 20 + 21 + 22 + 22 + 23) / 7 = 21
Sum of Squared Deviations = (19 - 21)2 + (20 - 21)2 + (20 - 21)2 + (21 - 21)2 + (22 - 21)2 + (22 - 21)2 + (23 - 21)2 = 4+1+1+0+1+1+4 = 12
Variance = 12 / 7 = 1.714
Standard Deviation = Square Root of 1.714 = 1.3
The standard deviation for a sample (the symbol is the letter s) is similar to the above, but the variance is computed by dividing the sum of squared deviations by the number of numbers minus one (n - 1). In Modules 1.4 and 1.5 we will adjust the sample size to n - 1 again, and refer to this as degrees of freedom. For large sample sizes, the impact of dividing by n - 1 versus dividing by n is negligible. For small samples, it makes a difference so dividing by n - 1 gives a larger or more conservative estimate of the spread. If the above set of data is a sample, the variance and standard deviation are:
Mean
= 21
Sum of Squared Deviations = 12
Variance = 12 /(7 - 1) = 2
Standard Deviation = S = Square Root of 2 = 1.4
The standard deviation is interpreted with respect to the mean. For symmetric bell-shaped sets of data, the interpretation of the standard deviation is:
95% (most) of the observations fall between the mean + 2 Std Dev
This can be combined with areas incorporating 1 and 3 standard deviations to completely describe a set of approximately symmetric, bell-shaped data:
68% of the observations fall between the mean + 1 Std Dev
95% of the observations fall between the mean + 2 Std Dev
99.7% (almost all or 100%) of the observations fall between the mean + 3 Std Dev
This very important property
is called the Empirical Rule - it applies to all symmetric bell shaped
sets of data. We will apply it later when we get to a larger example.
The third measure of spread or variation is the interquartile range
(IQR). To compute this measure, we need the 1st and 3rd quartiles (Q1 and Q3,
respectively). Twenty five percent of the ordered observations in a set of data
is contained within a quartile, so 25% of the observations are below the first
quartile, 50% of the observations are below the 2nd quartile (Q2, also called
the Median), and 75% of the observations are below the 3rd. The IQR is simple
Q3 - Q1. Here are the computations, using the numbers 19, 20, 20, 21, 22, 22,
24.
Q1 = (n + 1)/4 ordered observation = 0.25 * (7 + 1) = 2nd ordered observation which is the first number 20.
where "*" is symbol for multiplication
Q3 = 3*(n + 1)/4 ordered observation = 0.75 * (7 + 1) = 6th ordered observation which is the second number 22 in the ordered array.
IQR = Q3 - Q1 = 22 - 20 = 2 days
The middle 50% of the data falls within the IQR. Sometimes, analysts like to expand the location measure of spread by reporting the five number summary:
Minimum, Q1, Median, Q3, Maximum
Pause and Reflect
The standard deviation and the interquartile range are measures of spread or variation. The standard deviation is associated with the mean and is an accurate measure of spread for symmetric bell-shaped distributions. The IQR is generally associated with the median, and is an accurate measure of spread for non-symmetric distributions. With two numerical measures (mean and standard deviation; or median and IQR) we gain much knowledge about a data set - even data sets of thousands of numbers.
Relative
Measures
Symmetry
There are some quick
numerical measures than can be used to supplement frequency distribution charts
to determine if the distribution is symmetric, bell-shaped or skewed. They are:
Set
of Data is skewed to left if mean < median
Set of Data is skewed to right if mean > median
Set of Data is symmetric, bell shaped if:
Mean
is approximately equal to median
Empirical rule is met
IQR is approximately equal to 1.33 * Standard Deviation
We will try the above rules
of thumb when we illustrate the Excel descriptive statistics with a larger
sample later in this module.
Variation
The coefficient of variation is a useful tool when comparing the variation
of one distribution to that of another, especially if the distributions have
different units of measurement.
Coefficient
of variation = (standard deviation / mean) * 100%
For the example: (1.4 / 21) * 100% = 6.67%
Suppose another company
experiences mean cycle time of 21 in their supply chain as well, but the
standard deviation is 7 days. The coefficient of variation in this case is 33%,
which reflects a process with much greater variability than one with 6.67%
coefficient of variation.
Observations
Relative measures of observations are useful to give observations context
within a data set. The percentile is a relative measure of location for
a number in an ordered array. We already discussed examples of percentiles,
since the first quartile is actually the 25th percentile - 25% of the data in
an ordered array are below the 25th percentile. Perhaps you recall your
percentile score on college entrance exams. If you scored in the 90th
percentile on the SAT, 90 percent of the ordered scores were below yours. To find
the 90th percentile, order the observations, then compute 90th percentile =
0.90*(n+1) to find the ordered observation of interest. If n = 780, then we
would be looking for the 703rd number.
For distributions that are approximately symmetric, bell-shaped, the Z-Score
or Z- Value is a powerful relative measure for observations. The Z-Score
is simply the number of standard deviations an observation is from the mean. So
when we find the Z -Score of a number, we standardize that number. What
is the Z-Score for the number 19.6 in a distribution with a mean of 21 and
standard deviation of 1.4?
Z = (observation - mean)/standard deviation = (19.6 - 21)/1.4 = -1
We would say that the number
19.6 is 1 standard deviation from (to the left of) the mean of 21.
Z-Scores have associated probabilities. Do you recall that 68% of the
observations in a symmetric bell-shaped distribution fall between the mean and +
1 standard deviation? That "1" standard deviation is the Z-Score!
Note also the 68% - we can find the probability for getting any Z-Score as long
as the set of data is normal or is approximately symmetric bell-shaped. For
example, what is the probability of getting an observation less than 19.6 days?
We know that theoretically, the range of data from 19.6 to 22.4 days includes
68% of the data, and since we have to have 100% of the data accounted for, 100%
- 68% or 32% of the data must include numbers up to 19.6 and above 22.4. Since
we assume these distributions are symmetric, 16% of the data is up to 19.6 and
16% is above 24. So, for a symmetric bell shaped distribution with mean of 21
and standard deviation of 1.4, the probability of observing a number less than
19.6 is 0.16 or 16%.; the probability of observing a number greater than 19.6
is simply 100% - 16% or 84%.
Using
Excel for the Computations
We will use the Data
Analysis Tool and Statistical Functions to produce the descriptive
statistics we have discussed thus far in Module 1.3.
The quickest way to generate a family of descriptive statistics is to use the Data
Analysis Descriptive Statistics Tool. Lets use the data from Worksheet
1.2.1 in Module 1.2. First create a column of the cycle times as shown in that
Worksheet (or if you saved that example, copy C1:C31 to a new area of your
worksheet past the histogram, such as Column J). I placed the numbers in column
J, starting with the title "Time" in Row 1, and the 30 cycle times in
J2 to J31. The data doesn't have to be sorted to compute the descriptive
statistics, but it can be. Now select Tools from the Standard Toolbar,
then Data Analysis from the pulldown menu, then select Descriptive
Statistics and follow the dialog box requests as you did in creating the
histogram. For output options, select Summary Statistics and Confidence
Level for the Mean, leaving the confidence level default at 95%. I also
like to put the output close to my data and histogram if I created a histogram
for the data. Remember that you only have to enter one cell location for the
Worksheet 1.3.1
|
Cycle Time |
|
|
|
|
|
Mean |
21.07 |
|
Standard Error |
0.54 |
|
Median |
21 |
|
Mode |
21 |
|
Standard Deviation |
2.94 |
|
Sample Variance |
8.62 |
|
Kurtosis |
0.90 |
|
Skewness |
0.89 |
|
Range |
13 |
|
Minimum |
16 |
|
Maximum |
29 |
|
Sum |
632 |
|
Count |
30 |
|
Confidence Level (95.0%) |
1.10 |
We have discussed the Mean,
Median, Mode, Standard Deviation, Sample Variance, Range, Minimum,
Maximum, Sum and Count (number of observations). You may ignore Kurtosis
(a mathematical measure of the concentration of data around the center compared
to the tails of the distribution) and Skewness (a mathematical measure
of the symmetry of the distribution). You may ignore Standard Error and Confidence
Level for now, but we will use them in Module 1.4
The Descriptive Statistics tool provides everything we have discussed then,
except Q3 and Q1. To get these, we need to use the Function feature of
Excel. As for all Excel Functions, position the cursor in a cell or select the
cell in which you want the quartile, for example M31. Select Insert from
the Standard Toolbar, then Function, then Statistical (in
left box of Paste Function dialog screen), then Quartile (scroll down to
find Quartile in right box of dialog screen), then follow the dialog screen by
inserting the cell range for your data (e.g., L2:L30), and 1 for Q1. The
resulting cell formula is =QUARTILE(L2:L30, 1). Note that no labels are allowed
so I started the cell range with L2 rather than L1. You should get the results
in Worksheet 1.3.2. I repeated this process for the third quartile, Q3, which I
placed in M32. I also added the formula =(M32 - M31) in cell M33 to get the
interquartile range. I added the labels in cells L31, L32, and L33 for clarity
since the function feature does not insert the title of the function.
Worksheet 1.3.2
|
|
|
|
First Quartile, Q1 = |
19 |
|
Third Quartile, Q3 = |
22 |
|
|
3 |
|
|
|
Lets use the above
descriptive statistics to completely describe the set of data.
Location Measures of Center and Spread
Fifty percent of the ordered observations fall below the median of 21 days.
Twenty-five percent of the ordered observations fall below the first quartile
of 19 days; and 75% of the ordered observations fall below the third quartile
of 22 days. The interquartile range is 3 days from 19 to 22, representing the
middle 50% of the ordered observations. The five number summary is complete
when we add the minimum value of 16 and maximum of 29 days.
Arithmetic Measures of Center and Spread
The mean is 21.07, or simply 21 days depending on the accuracy we need for
reporting purposes. The standard deviation is 2.94 or, rounded, 3 days. The
interpretation: most or 95% of the observations fall within the interval: mean +
2 *s = 21 + (2 * 3) or 15 to 27 days. To use the Empirical Rule to
completely summarize a set of data which is approximately symmetric and
bell-shaped, and having a mean of 21 and standard deviation of 3:
68% of the observations are within 21 + (1 * 3): 18 to 24 days.
95% of the observations are within 21 + (2 * 3): 15 to 27 days.
100% of the observations are within 21 + (3 * 3): 12 to 30 days.
From the above, we would not
expect any observations below 12 days or above 30. Such observations would be
outliers.
Percentile
To find the percentile using Excel, select Insert on the Standard
Toolbar, then Function, then Statistical, then Percentile,
and then respond to the dialogue box by entering the cell range for your
numbers and the desired percentile. For example, to get the 25th percentile for
this illustration, the resulting cell formula will be:
=PERCENTILE(L2:L31,0.25). The percentile will be placed in your spreadsheet
wherever you have the cursor (active cell). (In
Excel 2007 you must first select the Formulas
tab before proceeding to the Insert Function option)
The Z-Score
What is the Z-Score for the number 18?
Z-Score = (number - mean)/standard deviation = (18 - 21)/3 = -1
So, 18 is one standard deviation to the left of the mean of 21. What is the Z-Score for the number 24?
Z-Score = (24 - 21)/3 = 1
The number 24 is one standard
deviation to the right of the mean. To get the Z-Score from Excel, we use the Standardize
function. Position the cursor or point and click in a cell in which you want to
place the Z-Score, such as Q2. Select Insert from the Standard Toolbar,then Function (REMEMBER: in Excel
2007 you must first select the Formulas
tab before proceeding to the Insert Function option), then Statistical, then Standardize
and respond to the dialog box questions. You should replicate the cell formula
=STANDARDIZE(18,21,3) which gives a Z-Score of -1. I actually prefer to use the
cell address for the number 18 so that I can copy the standardize cell
reference to standardize a whole row or column of numbers. This would be
=STANDARDIZE(L6,21,3). I then add a title to the column, such as
"Z-Scores." The fifth requirement in Project Assignment 1 is to
standardize (generate Z-Scores) for your column of data.
Z-Scores are very handy ways of identifying outliers. Any Z-Score below -3 or
above +3 would identify a number more than 3 standard deviations from the mean.
The sixth requirement in Project Assignment 1 is to remove any outliers from
your data, and re-compute the descriptive statistics. Outliers are quickly
identified by Z-Scores. Removing an outlier from a real data set doesn't mean
we can ignore it for analysis - it just means we should analyze it separately
from the data.
A side note: to remove a data element from a column of numbers in Excel means
to remove it, not type over the number with a zero. To remove a number, point
and click to it, select Edit on the Standard Toolbar, then Clear
from the pulldown menu, then select Contents. This creates a blank space
where the number once resided. If you want to remove the number and the space,
select Edit, then Delete from the pulldown menu, then check Shift
cells up if you have a column of data, or Shift cells left if you
have a row of data.
The Probability for the Z-Score
Excel has a statistical function that automatically computes the
probabilities for Z-Scores. Let's find the probability of getting a cycle time
below 18 days (remember, time is a continuous variable, so a number below 18
could be 17.9999). If you know the Z-Score for a number, the NORMSDIST
function will give a cumulative probability for the area under a symmetric
bell-shaped distribution up to that Z-Score. NORMSDIST stands for
Standardized Normal Distribution. Position the cursor or point and click in a
cell in which you want the probability. Select Insert, then Function,
then Statistical, then NORMSDIST and simply enter the Z-Score
of -1. You should get 0.158655 or 0.16 or 16%. The probability of obtaining an
observation less than 18 days is 0.16 or 16%. What is the probability of
obtaining an observation GREATER than 18? You guessed it: 100% - 16% = 84%.
The seventh item in Project Assignment 1 is to compute the probability of
exceeding the 45th ordered (sorted) observation in your data set. If you have
more or less than 50 observations, compute the process capability for the 5th
from the last ordered observation.
There are some alternative Excel procedures and manipulations, but we have
described the important basics. What if you want the probability of getting a
cycle time below 18 days but do not know the Z-Score? Use the Excel Function NORMDIST
function. Point and click to a cell where you want the probability, select Insert
from the Standard Toolbar, then Function, then Statistical, then NORMDIST
and respond to the dialog box questions by entering the number, mean, standard
deviation and the work TRUE). The cell formula would look like this:
=NORMDIST(18,21,3,TRUE).
The Normal Distribution
Before we close this set of notes with one more example, let me say a few words
about the normal distribution. The mean, standard deviation, Z-Scores and
normal probabilities or probabilities for Z-Scores all depend on the
distribution being approximately symmetric bell-shaped or "Normal".
The distributions will never be perfectly bell-shaped in real life, but they
don't have to be - approximately normal is fine, especially if we have at least
30 observations. So, how do you know if the distribution is normal? Here are
some general rules of thumb:
1). Check
the histogram to see if it has a symmetric bell shape, without outliers (any
observation with a Z-Score greater than +3 or less than -3).
2). The mean should be approximately equal to the median. For this example,
21.07 is approximately equal to 21.
3). The interquartile range should be close to 1.33 times the standard
deviation. Here, the IQR of 3 is fairly close to 1.33 times 2.94 (3.9) although
we would like this somewhat closer.
4). Check theoretical ranges of the empirical rule and compare them to the
actual data.
68%
of the data should be between 18 and 24. The actual count is 26 out of 30 or
80%.
95% of the data should be between 15 and 27. The actual count is 29 out of 30
or 96.7%.
100% of the data should be between 12 and 30. The actual count is 30 our of 30,
or 100%.
Most of the rules of thumb
work for this cycle time example. Let’s look at an example where there is an
outlier.
Putting
it Together with One More Example
What if the 31st
observation was 38? We already know that 100% of the observations should fall
within the range of 12 to 30, so 38 is more than 3 standard deviations from the
mean - do you remember what we called that - yes, an outlier or a signal.
Process Control Chart
Suppose you created a process control chart to monitor the cycle time
process based on the original 30 observations. The mean of the chart is 21, the
upper control limit for a process is the mean plus three standard deviations or
21 + (3 * 3) = 30. The lower control limit is the mean minus three standard
deviations or 21 - (3 * 3) = 12. These are upper and lower control limits for
processes since we expect nearly 100% of the observations generated by a
process to be within the area of the mean + 3 Std Dev. The Upper
Specification Limit of 24 is set by the boss or the customer, or whomever - it
is not set by statistics. Here is the process control chart:
Worksheet 1.3.3
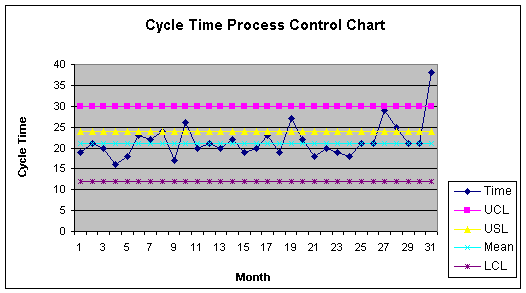
Note that the 31st observation is above the UCL and would justify investigation as a signal that the process has gone out of control. Let's confirm this with finding the probability of getting an observation of 38 or greater, with a process mean of 21 and standard deviation of 3. First, the Z-Score computation:
Z-Score = (number - mean)/Std Dev = (38 - 21)/3 = 5.67
Now, find the probability using NORMSDIST function of Excel. The cell formula is:
=NORMDIST(5.67) = 0.99999999
Recall, this is the cumulative
probability of observing a number LESS than 38. So to get the probability of
observing a number greater than 38, take 1.0 - .99999999 = 0.00000001 or there
is a 0% probability of observing a 38 if the mean is 21 and the standard
deviation is 3 - that's why its called a signal or outlier.
Before leaving the process control chart, let's focus for a moment on the upper
specification limit set usually by the boss or customer. The USL is 24. Way
back at the beginning of this note set, Module 1.1, we indicated that there is
no way we can please the boss with an upper specification limit of 24. Now you
should be able to say why that is so. With a mean of 21 and a standard
deviation of 3, we know that 24 is +1 standard deviations from the mean ( z-
score = (24 - 21)/3 = + 1). The probability of getting an observation above 24
is found by first getting the probability of a number less than 24:
=NORMDIST(+1) = 0.84
This process is only capable
of satisfying the customer 84% of the time - that is a measure of process
capability. Now, to get the probability of finding a number above 24: 1.0 -
0.84 = 0.16. There is a 16% probability of getting an observation above 24 -
that is why the customer will not be pleased. An upper specification limit one
standard deviation above the mean is a 1 sigma process - GE's goal is to have
SIX SIGMA processes - specification limits 6 standard deviations from the mean.
Descriptive Statistics
What if you were just starting out and collected 31 observations and had no
prior knowledge of the mean, standard deviation, median, IQR or histogram. You
would first generate the histogram, as shown in Worksheet 1.3.4 below.
Worksheet 1.3.4
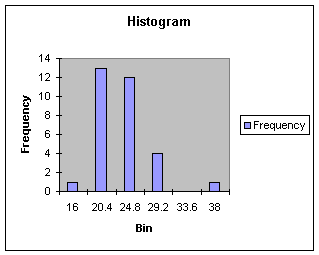
By observation, we would say
there is an outlier to the right of the range of the data, thus making a
distribution that is skewed right. If we needed to report the center and
spread of the skewed distribution we would use the....... that's right, the
median and interquartile range. Here are the descriptive statistics:
Worksheet 1.3.5
|
Time |
|
|
|
|
|
Mean |
21.61 |
|
Standard Error |
0.75 |
|
Median |
21 |
|
Mode |
21 |
|
Standard Deviation |
4.19 |
|
Sample Variance |
17.58 |
|
Kurtosis |
7.04 |
|
Skewness |
2.22 |
|
Range |
22 |
|
Minimum |
16 |
|
Maximum |
38 |
|
Sum |
670 |
|
Count |
31 |
|
Confidence Level(95.0%) |
1.54 |
|
1st Quartile = |
19 |
|
3rd Quartile = |
22.5 |
|
|
3.5 |
Using this data, we see that the mean is now greater than the median, confirming the right skew. Note that the median remains 21, as with the original data set. The mean is larger since the outlier is pulling it to the right. Note also the standard deviation is 4.19 or 4.2 which is considerably inflated from the original data with its standard deviation of 3. Outliers always increase the standard deviation. To confirm that 38 is an outlier with this data, we standardize:
=STANDARDIZE(38,21.6,4.2) = 4.05
Thirty-eight is more than 3
standard deviations from the mean. In a real project, we would segregate the 38
from the rest of the data, investigate and make corrections, and redo the
descriptive analysis without the outlier. This is precisely what you may have
to do with your data in Project Assignment 1. Item 5 is to standardize your
data, Item 6 is to remove outliers and re-compute the descriptive statistics.
Data without outliers is likely to be symmetric, bell shaped if there was no
bias in data collection. Inferential statistics for the mean of a distribution,
which includes confidence intervals and tests of hypothesis, work best with
symmetric bell shaped distributions. These subjects are covered next in Modules
1.4 and 1.5.
Optional
Material on the Mean
This module focused on the arithmetic mean, the typical measure of central
tendency, and the measure used in inferential statistics. There are two other
means I should briefly mention: the weighted mean, and the geometric mean.
Weighted
Mean
The weighted mean is
a special case of the arithmetic mean used when there are several observations
of the same value. Suppose you had cycle times of 21, 23, 19, 22, and 20, which
gives an arithmetic mean of 21 days. But suppose further that cycle time 21
happened 20 times, 23 happened 5 times, 19 happened 50 times, 22 happened 10
times, and 20 happened 15 times. The mean cycle time weighted by frequency of
occurrence, or simply the weighted mean is:
Weighted mean = sum of weights * observation / sum of weights
where weights are frequency of occurrence in this example
Weighted mean = (21*20 + 23*5 + 19*50 + 22*10 + 20*15) / 100 = 20
Geometric
Mean
The geometric mean
applies when we are interested in computing the mean for interest and growth
rates, percentages, and ratios (Mason, 1999). Suppose you have a CD paying 10%
interest in Year 1 (I wish!), and then 4% interest in Year 2. The arithmetic
mean interest rate is
Mean interest rate, i = (0.10 + 0.04 ) / 2 = 0.07 or 7 %
However, to take into account the compounding effect, the geometric mean gives
a more precise outcome:
Geometric
mean = ![]() where i is
the interest in each year and n is
the number of years.
where i is
the interest in each year and n is
the number of years.
=
![]() = 1.0696 or 6.958 %
= 1.0696 or 6.958 %
Let's check this with $95,000:
95,000
* 0.10 = 9500 (Year One)
(95000 + 9500) * 0.04 = 4180 (Year Two)
Total Interest = 9500 + 4180 = 13680
The geometric mean: 95000 * 0.06958 = 6610
(95000 + 6610) * 0.06958 = 7070
Total Interest = 6610 + 7070 = 13680
The arithmetic mean:
95000 * 0.07 = 6650
(95000 + 6650) * 0.07 = 7115
Total Interest = 6650 + 7115 = 13765
The geometric mean gives the truer figure in recognition of the compounding
effect. In general: geometric mean = ![]() where all x values must be positive.
where all x values must be positive.
A second application of the geometric mean is to find the percent increase, or
growth rate, over time. Suppose the University gave the
(5 years – 1) = 4, and
= ![]() – 1
– 1
= ![]() - 1
- 1
= .1725 or 17.25%
Reference:
Anderson, D., Sweeney, D.,
& Williams, T. (2006). Essentials of Modern Business Statistics with
Microsoft Excel.
D.
Groebner, P. Shannon, P. Fry & K. Smith.
Business Statistics: A Decision Making Approach, Seventh Edition,
Prentice Hall, Chapter 3
Ken
Black. Business Statistics for Contemporary Decision Making. Fourth Edition,
Wiley. Chapter 3
Mason,
R., Lind, D. & Marchal, W. (1999). Statistical Techniques in Business
and Economics (10th. ed.).
| Return to Module Overview | Return to top of page |