Notes on Chi-Square
|
Practice Set
|
|
Chi-Square -- Step
1
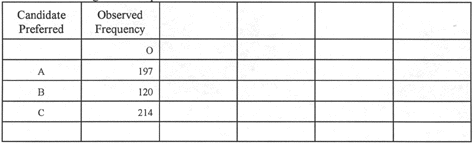
The Null Hypothesis: There will be no
difference in the number of votes for each candidate.
The first step is to enter the observed
number of votes for each candidate.
Then look up in a Table of Chi-Square
values to determine what value is the cutoff for rejecting the null hypothesis.
The degrees of freedom for three candidates is the number of candidates
minus one. For this example, the degrees of freedom is 2. For an alpha
of .05, degrees of freedom of 2, and a two-tailed test, the Chi-Square
value will need to be greater than 5.992.
|
Table 1
|
|
Chi-Square -- Step
2
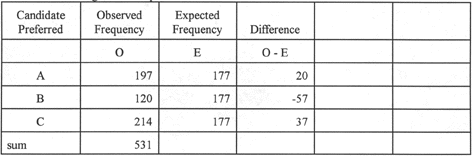
The second step is to total the number
of observed frequencies and divide it by the number of candidates. The
result is the expected frequency for each candidate. This is the expectation
by chance. In this example, 197 + 120 + 214 = 531. Then, 531 / 3 = 177.
|
Table 2
|
|
Chi-Square -- Step
3
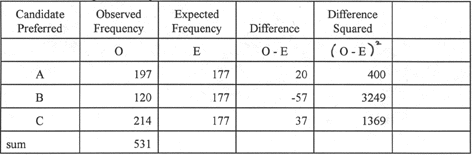
The third step is to subtract
the expected frequencies from the observed frequencies. The results are
difference scores.
|
Table 3
|
|
|
Table 4
|
|
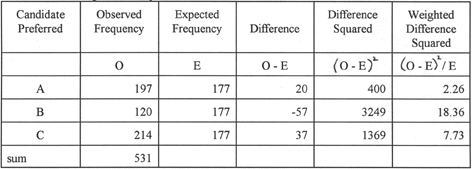
Chi-Square -- Step
5
The fifth step is to divide each squared
difference score by the expected frequency. The results are weighted squared
difference scores.
|
Table 5
|
|
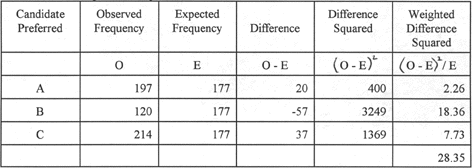
Chi-Square -- Step
6
The sixth step is to sum the weighted
squared difference scores. The result is the Chi-Square value.
|
Table 6
|
|
Chi-Square -- Step
7
Our result now needs to be evaluated
based on the Chi-Square value we determined in the first step, from the
table to be our cut off for rejecting the null hypothesis.
REMINDER:
When we looked up in a Table of Chi-Square
values to determine what value is the cutoff for rejecting the null hypothesis,
using the degrees of freedom of 2, and an alpha of .05, the Chi-Square
value needs to be greater than 5.992.
Our obtained Chi-Square value of 28.35
is greater than 5.992; so we reject the null hypothesis.
REMINDER:
The Null Hypothesis: There will be no
difference in the number of votes for each candidate.
Interpretation: The number of votes
received by each candidate was not a factor of chance.
Return
to Module 9 Notes
|
Part II:
Chapter 3 Experimental and Quasi-Experimental Research 
