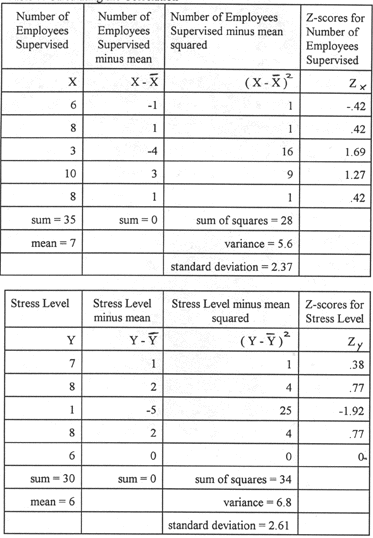
The sixth step is to convert all the scores to z-scores. Remember, to do this you must take the raw score, subtract the mean, and divide by the standard deviation. In the second column, we have the raw score minus the mean for the variable AX. So if we take these and divide them by the standard deviation for AX (2.37), we will have the z-scores for AX. 

In the ninth column, we have the raw score minus the mean for the variable AY. So if we take these and divide them by the standard deviation for AY (2.61), we will have the z-scores for AY. 

Be careful of your signs. Remember, if you divide a positive number by a positive number, you get a positive number. If you divide a negative number by a positive number, you get a negative number. 
 

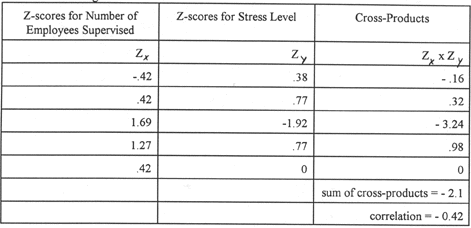
The seventh step is to multiply the z-scores for AX by the z-scores of AY. The results are called cross-products.  
Remember your signs: if you multiply two negative numbers together, you get a positive number. If you multiply two posititive numbers together, you get a positive number. If you multiply a positive number and a negative number, you get a negative number.  

The eighth step is to sum these. The result is called sum of cross-products. Remember your signs. The easiest way I have found to do this is to add all the positive numbers together (here you would get 4.54). Then add all the negative numbers together (here you would get -.16). Then do 4.54 - .16). 

Then divide the sum of cross-products by the number of cross-products (here we have 5). 

This is called the correlation!  

In the first step where you plotted the scores creating a scatter plot, did you determine that the correlation would be positive? Did you determine that the correlation would be strong?