|
Index to Module Two Notes
|
Let
me introduce an article explaining how Module 2 is used in practice: Do Your Assets Correlate?
“Investors
are increasingly preoccupied with the relationship between U.S. and foreign
markets, particularly last Thursday, when a 4.5% drop in the Shanghai Composite
Index led to declines across Asia. U.S. markets finished flat or slightly
lower.” Textbook theory suggests that
investing abroad helps to diversify a portfolio because overseas stocks are
influenced, at least in part, by local economic conditions and interest rates.
Therefore, they shouldn't necessarily move the same way as U.S. stocks. “During
the two-year period that ended in February, correlation between U.S. and other
developed markets was 0.63, according to ING Asset Management. That is a big
decline from 2003 to 2005, when they practically moved in lockstep, at 0.93.
(The figures are based on monthly movements in the Standard & Poor's
500-stock index and the Morgan Stanley Capital International EAFE indexes.)”
Asset correlation is commonly
mentioned in investment discussions but seldom explained in detail — even
though it is critical for any diversification strategy. Allocating to different assets (such as stocks
and bonds) that tend to move up and down under different market conditions may
help you offset one asset’s falling returns with another’s rising returns. This
is the basic idea behind asset correlation, a strategy designed to potentially
lower investment volatility, with the goal of improving the portfolio’s
diversification.
How Asset Correlation
Works: In portfolio management theory, correlation
statistically captures the relationship between two variables. It shows
whether, and how strongly, selected assets are related. It measures how much the returns of any two
or more securities are related, but does not imply that the movement of one
security causes the movement of another, or that this relationship will exist
in the future. “Securities” is another word for investments.
Correlation
ranges from +1.0 to –1.0, where +1.0 equals perfect positive correlation, –1.0
equals perfect negative correlation and 0.0 equals zero correlation.
Positive Correlation: Assets with a perfect positive correlation
have a perfect linear relationship, which means that by knowing how the return
of one security behaves (rises or falls), you will be better able to forecast
what the other security will do. For example, if security A’s return goes up,
you can expect security B’s return to rise as well; you just can’t know by how
much.
Negative Correlation: With perfect negative correlation, the funds’
returns move opposite to each other. If one fund has a positive return, you can
anticipate that the other fund will have a negative return.
Zero Correlation: With zero correlation, there’s no
relationship between the returns of the selected securities. As a result, the
returns of one security are not an indicator of the returns of another.
In
this module we will present and describe linear relationships as described
above. Correlation analysis involves the study of the strength
of the relationship between two variables. A supporting role of correlation
analysis is to discover those explanatory variables that are strongly related
to the response variable to improve the predictions made. For example, suppose
we want to predict the number of hours it would take to perform an audit on a
client. One explanatory variable might be be the dollar amount of client
assets. Another explanatory variable might be the number of employees. After
gathering and analyzing data we discover that the correlation between hours and
assets is much higher than between hours and employees. In this case, we would
be better off using assets as the explanatory variable.
Regression analysis involves the study of the form
and direction of the relationship between two or more variables. The
main purpose of regression analysis is to predict the value of a dependent
or response variable based on values of the independent or explanatory
variables. Simple linear regression analysis involves the study of the linear
or straight-line relationship between two numerical variables: the dependent
variable and one numerical explanatory variable.
This set of module notes introduces techniques for presenting and describing
simple linear regressions and correlations. Module 2.2 Notes describe how we
test linear regressions for statistical significance and practical utility, and
how the linear regression model can be used for prediction. The outline of
steps to conduct a complete simple linear regression and correlation analysis
is:
1.
Hypothesize the regression model relating the dependent and independent
variables.
2. Gather data and describe the form and direction of the relationship with a
scatter diagram.
3. Estimate the regression model parameters and the correlation coefficient.
4. Test the practical utility of the regression model.
5. Test the statistical utility of the regression model.
6. Evaluate the assumptions of the regression model.
7. Use model for prediction.
This set of module notes will
carry us through Steps 1 through 3 above. Module 2.2 Notes will cover Steps 4
through 7. In Module 3 we will expand this model to consider the relationship
between the dependent variables and multiple independent variables, including
nonlinear terms and categorical variables.
Step 1:
Hypothesize the Regression Model Relating the Dependent and Independent
Variables
The dependent or response
variable, identified by the symbol Y, is the variable we wish to predict. The
independent or explanatory variable, identified by the symbol X, is the
predictor variable. In simple linear regression, we propose the following
population straight-line model relating Y and X:
Eq. 2.1.1: Y = B0 + B1X + e, where:
Y
= Dependent Variable
X = Independent Variable
B0 = Y Intercept=mathematical value of Y when X=0
note: Unless there are X values of 0, the Y intercept has no practical interpretation, just a mathematical interpretation as we will see later with an example.
B1 = Slope = the amount of increase in Y (or decrease if
B1 has a negative sign) when X increases one unit .
e = Random error
For a particular observation, for example the "ith" observation, this equation becomes:
Eq. 2.1.2: Yi = B0 + B1Xi + ei
This equation implies that each observation in a set of data has an actual Y value, an X value, a predicted Y value, and error which is the actual Y value minus the predicted Y value. In regression analysis, one of our objectives is to select those predictor variables that result in as little error as possible, recognizing there will always be some error in prediction. This equation is often referred to as the probabilistic model relating Y to X. The deterministic model is just the straight-line or prediction part without the actual value of Y and its error:
Eq. 2.1.3: E(Y) = B0 + B1X, where
E(Y) = Expected Value of Y
In step two, we will fit a
straight-line model based on sample data to estimate the above simple linear
regression equation.
That's enough theory. Let's go to step two, look at some data, and create the
scatter diagram.
Step 2:
Gather Data and Describe the Form and Direction of the Relationship with a
Scatter Diagram
The example to illustrate
simple linear regression analysis is about a audit company - that is, a company
that is in the business of performing financial audits. This company maintains
a very small internal workforce and thus relies of external auditors to perform
client audits. The company would like a model to predict the number of external
audit hours it would need to contract in order to do an audit. Such a model
would be very helpful in budgeting and planning. Management believes that a
good predictor variable would be client assets. In order to build the model, a
sample of data must be gathered.
Worksheet 2.1.1 shows the
result of the sample. The first column, Assets, are values of the independent
variable (this is the X variable) in thousands of dollars. The second column,
ExtHours, contains values of the dependent variable (this is the Y variable) in
hours. So, the first row of numbers represents an audit completed in the past
for a client with assets of $ 3,200,000. The audit company had to contract for
700 external hours to perform the audit. Note that in regression analysis, every
observation has two values, an X value and a Y value.
Worksheet 2.1.1
|
Assets |
ExtHours |
|
3200 |
700 |
|
3000 |
900 |
|
3500 |
800 |
|
4000 |
900 |
|
4700 |
880 |
|
5000 |
850 |
|
6000 |
1000 |
|
5500 |
1000 |
|
6500 |
950 |
|
6500 |
1100 |
|
7000 |
1200 |
|
4500 |
830 |
|
7500 |
1100 |
|
5750 |
1100 |
|
7250 |
1160 |
|
8000 |
1120 |
|
8000 |
1300 |
|
8500 |
1400 |
|
9000 |
1500 |
|
8500 |
1200 |
In the Assignment section of the
Main Module 2 web page, you will see that the first item for Assignment 2 is
entering the X and Y data in an Excel Spreadsheet. Hopefully, you can think of
a good response variable from your work , service or home environment. Perhaps
you would like to predict profit contribution, sales, or salary, or hours to
complete a task. Once you determine what you would like to predict or
understand, then pick a variable that you think explains or predicts your
response variable. Perhaps labor cost is a good X (cost driver) to predict
profit contribution (Y). Perhaps years of experience is a good X variable to
predict salary (Y). Once you select your X and Y variables, try to collect 50
observations. In regression and correlation analysis, an observation involves
an X and a Y value. For example, sales in month 1 were 334 units. Here, 1 is
the value for X and 334 is the value for Y for the first observation. Another
example, an employee in the database earns $50,000 (the value of Y for this
sample observation) and has worked for 22 years (the value of X for this sample
observation). Fifty observations is more than the minimum required, so you can
get by with less if you have to. The minimum required for a two-variable
regression model is 20 observations (10 observations per variable). The next
task is to create the scatter diagram.
In regression analysis, the scatter diagram is used to plot the
independent variable on the X or horizontal axis, and the dependent variable on
the Y or vertical axis. To produce a scatter diagram, highlight the X and Y
data columns including the column titles. Then select the Chart Wizard on the
Standard Toolbar, then from the Chat menu select , then XY Scatter, (in Excel 2007,
select Insert from the menu tab, then Scatter from the Chart option),
then respond to the dialog screen questions. It will take a couple of tries to
get the hang of making scatter diagrams; but after some practice you should be
able to replicate the scatter diagram shown in Worksheet 2.1.2. In Assignment
2, the second item is for you to create a scatter diagram.
Worksheet 2.1.2.
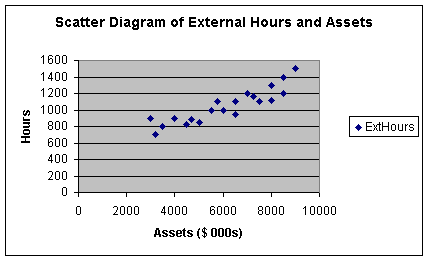
Note that as I was going through the dialogue boxes, I used the opportunity to
label the X and Y axis's, as well as give the diagram a title. This scatter
diagram shows a positive form of relationship between X and Y, meaning
that when X increases, Y increases. It appears that when X increases, Y
increases at a constant rate, meaning that the form of the relationship
is linear.
A comment on page presentation. If you click on File on the Standard
Toolbar, then Print Preview, you can see where the scatter diagram will
appear on the worksheet page. If you want to move it, just click on any part of
the white area of the diagram and click and drag the chart. If you want to
change the shape of the chart, click on the chart again and note the squares
along the borders of the chart. If you click and drag on the middle squares you
can make the chart wider, narrower, longer or shorter. Note finally that when
you click on any chart, the word Data changes to Chart on the
Standard Toolbar so you can switch between data functions and chart functions.
Let's summarize what we have learned thus far. Regression analysis includes the
study of the form and direction of the relationship between dependent and
independent variables. In this case, we have one dependent (Y) and one
independent variable (X). The form of a relationship can be linear or
curvilinear. The form in Worksheet 2.1.2. above happens to look like a linear
relationship. Worksheet 2.1.3 illustrates a curvilinear relationship.
Worksheet 2.1.3
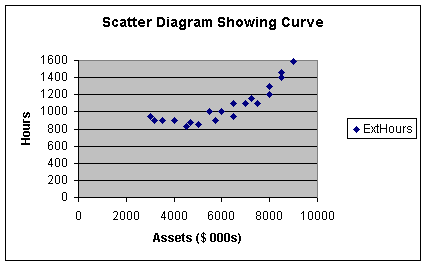
Note with the curvilinear relationship, as assets increased initially, external
audit hours remained relatively constant up to clients with assets of
approximately $5,000,000. Then it appears that external hours increase at a
slightly increasing rate from $5,000,000 to $9,000,000. We will see in Module 3
that this is curvature: Y increases at an increasing rate as X
increases. Curvature also occurs when Y increases at a decreasing rate
as X increases.
Before continuing with the example, let's summarize the direction
component of the relationship. Our example in Worksheet 2.1.2 shows a positive
direction. Worksheet 2.1.4 shows what a negative direction would look like.
Worksheet 2.1.4
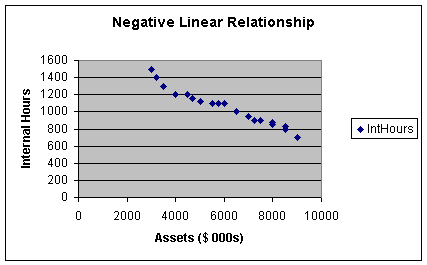
In this worksheet, as assets increase, internal hours decrease: this describes
a negative relationship between X and Y.
Pause
and Reflect
To describe the
relationship between two variables, we look at the form (linear or
curvilinear) and the direction (positive or negative) of the
relationship. Linear form means that as X increases, Y increases or decreases
at a constant rate. Positive direction means that Y increases when X increases;
and negative direction means that Y decreases when X increases.
The last component of the
relationship between two variables is strength. We will talk about measuring
strength in Step 3, as we need some numbers to do that.
Step
3: Determine the Simple Linear Regression Equation and Correlation Coefficient
Regression
Coefficients
Our next step is to find values for b0 and b1 in the
following simple linear regression equation:
Eq. 2.1.4: y = b0 + b1x
This equation, based on
sample data, is used to estimate the hypothesized population Eq. 2.1.3. Note I
have made all of the symbols lower case to distinguish the sample equation from
the population equations shown as Eq. 2.1.1. - Eq. 2.1.3. Some texts put hats (
^ ) on the symbols in Eq. 2.1.4 to distinguish the sample equation from the
population model. Our task is to estimate numerical values for the intercept, b0,
and the slope, b1. These are called the regression parameters in the
simple linear regression equation (the equation is also known as the least
squares regression equation or the trend equation or simply the regression).
If you were a careful artist, you could take a ruler and draw a straight-line
as close as possible to every point in Worksheet 2.1.2. Then, extend the left
end of that line to the Y axis. The y value at the point where an extension of
the line touches the Y axis is called the intercept, the value of y when x
equals zero. Next, anywhere on the line, draw a horizontal line one unit long
in the X direction. Now draw a vertical line to the regression equation. The
length of the vertical line divided by the length of the horizontal line
represents the amount of change in Y for the unit change in X. This is called
the slope of the line. Don't be alarmed - we will let the computer do the
"line drawing" to estimate the slope and the intercept - I just
wanted to go over the concept.
Actually, the computer uses mathematics to solve equations to determine the
value of the slope and intercept. The technique is called the least squares method of regression. It
essentially involves trying to minimize the error (actual value of Y minus the
predicted value of y) in the equation Sum (Y - y)2. To let Excel do
the work, first make a copy of the scatter diagram to preserve the original. To
copy the diagram, put the cursor anywhere in the white area of the the scatter
diagram chart. When you click the left mouse button, the chart becomes
highlighted (small squares or handles appear around the border of the chart).
Now select Edit on the Standard Toolbar and Copy from the
pulldown menu. Now move the cursor, select a new cell of the worksheet, and
select Edit on the Standard Toolbar and Paste from the pulldown
menu. You should get another copy of the scatter diagram.
Now select (highlight) the copy of the scatter diagram by clicking anywhere on
the white chart surface and select Chart on the top menu bar. Note that
this menu bar has the word Data instead of the word Chart unless
you have highlighted a chart, such as the scatter diagram. Next select Add
Trendline from the pulldown menu and you will get a dialog box. The default
Linear trend/regression is what we want. Before selecting OK, select the
Options Tab. Then select Display Equation and Display R-Square.
You should get Worksheet 2.1.5, as shown below.
Excel
2007 has a redesigned dialogue box but the sequence of steps is the same.
Worksheet 2.1.5
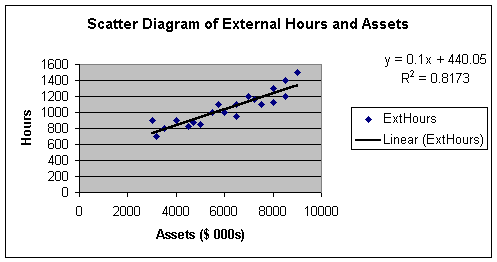
The least squares regression equation, or simply, the linear regression
equation, is shown as:
Eq. 2.1.5: y = 440.05 + 0.1x, since y is ExtHours and x is Assets,
ExtHours = 440.05 + 0.1(Assets).
After we finish Steps 1- 6, we will use this equation to make a prediction. To jump ahead, what if we want to predict the hours it will take to audit a company with $6,000,000 in assets. Looking at the Worksheet 2.1.5 regression line, if we go straight up from 6000 on the X axis, we touch the line at a y value a little over 1,000 hours. To be more accurate, we can substitute 6000 into Eq. 2.1.5 and get:
Eq. 2.1.6: y = 440.05 + 0.1 (6000) = 440.05 + 600 = 1040.05.
Note carefully that I
substituted 6000 into Eq. 2.1.6 rather than 6000000 since the original data was
entered in thousands.
However, before we use the equation for prediction we have to test it's practical
and statistical utility (Steps 4 and 5). For now, let's be sure we understand
how to interpret the equation. The intercept is 440.05. This
means that the value of y (External Hours) is 440.05 when x (assets) equals
zero. Now this is really just a theoretical point helpful in placing the
equation on the scatter diagram. It is theoretical without practical value
because we did not have any x (asset) values equal to zero in the original
data. Some suggest that the intercept is like a fixed value - what we need to
get started without any value for x at all. But to know this, we would have had
to include observations where x in fact equals zero. Otherwise, we are just
guessing. In fact, an ethical caution in regression is not to
interpret the results of regression models outside of the range of the original
data.
Now let's look at the slope, which is 0.1. The slope is interpreted
as follows: y (External Hours) is predicted to increase 0.1 when x (assets)
increase by one. To make this a bit more practical, we can say that External
Hours increase by 0.1 when Assets increase by $1,000 (since our data was is in
thousands of dollars, 1 unit of x is equal to $1,000). Since the relationship
is linear and the coefficients are proportional, we can also say that external
hours increase by 1 when assets increase by $10,000; or external hours increase
by 10 when assets increase by $100,000; or external hours increase by 100 when
assets increase by $1,000,000. Now we have something! The firm should plan on
100 more external hours for every increase of $1,000,000. Caution as before:
this interpretation only applies within the range of our data. We don't know
what the slope is above $9,000,000 since we did not have any observations above
$9,000,000. We do not extrapolate beyond the range of our data when making
interpretations.
Pause
and Reflect
The intercept in
the regression equation is the value of y when x equals zero. It has no
practical interpretation unless the regression model was built on data where
some of the values of x were zero. The slope of the regression equation
indicates the predicted change in y (increase if the slope is positive;
decrease if the slope is negative) for a one-unit increase in x.
Regression equations are the
most widely used statistical tools in business since they can be used to
predict the value of a response variable, such as sales, based on a predictor
variable. We discussed form and direction as important aspects of
the relationship between the two variables. The strength of the
relationship between two variables is also an important aspect to know about in
business.
Correlation Analysis
Recall earlier that we said correlation analysis is used to measure the
strength of the linear relationship between two quantitative variables. To find
the correlation coefficient, we begin with the coefficient of determination, R2.
Look back at Worksheet 2.1.5 and note the R2 = 0.8173 or 0.82 on the
scatter diagram. R-Square, or R2, is the symbol for the coefficient
of determination. We will see its math later. For now, the interpretation of R2
is simply the amount of sample variation in Y that is explained by X. For my
example, we would say that client assets explain 82% of the sample variation in
external hours.
As you look at a scatter diagram you notice that the value of Y changes or
varies for different values of X. Strongly related variables are those in which
changes in X result in predictable changes in Y. In other words, X is
explaining a large percent of the variation in Y. Weakly related variables,
such as those with R2 below 25%, suggest that changes in X do not
result in predictable changes in Y. We will have more to say about R2
when we get to Step 4 in Module 2.2 Notes. I'll close this brief introduction
with the note that R2 should be as close to 100% as possible in
order for us to have models that are practically useful. A good general
benchmark is that R2 should be at least above 50%, although it
should be noted that specific industries/service sectors may have their own
traditional benchmarks for R2.
The correlation coefficient, r, is the statistic commonly used to report the
strength of a linear relationship between two variables. In fact, the word has
crept into common English usage when we say something like, "there is a
high correlation between how much I study and my GPA" (at least I hope we
say something like that!). The correlation coefficient is simply the square
root of R2. For this example, r = +0.904.
This r of +0.904 represents a strong, positive, linear relationship between client
assets and external hours. How do I get the direction? By looking at the
sign on the slope coefficient. If the sign is positive, r is positive, and
vice-versa. Worksheet 2.1.4 shows a relationship in which the r would have a
negative sign. How do I get the measure of strength? That one is tougher
but here are some benchmarks that are common in general business/service
sectors (you may find different benchmarks in medical practice, psychology, and
specific industries/service sectors, and so forth):
r = -0.9 (and below): Strong negative linear relationship
-0.7: Moderate negative linear
relationship
-0.5: Weak negative linear relationship
+0.0: No relationship
+0.5: Weak positive linear relationship
+0.7: Moderate positive linear relationship
+0.9 (and above): Strong positive linear relationship
There are two cautions with
using the correlation coefficient. First, we can say that X and Y are strongly
related, which implies that changes in X result in predictable changes in Y.
But unless we do an experiment, we are cautioned against saying that X causes
Y from an ethical perspective. Think about examples of this. The r between
consumption of the alcohol beverage Scotch and donations to charitable
organizations is very high, such as above a positive 0.90. We would not say
that such consumption causes donations to increase, or reduced consumption
causes donations to decrease because the causation variable is probably
disposable personal income. When DPI goes up, donations and consumption go up.
That being said, we can still rely on the value of r to select variables that
have an impact or result in a change in Y, without having to do an experiment.
That is, marketing executives in the Scotch industry can still pattern sales
projections off projections of aggregate donations to charitable organizations
- to make predictions, you do not have to prove causation.
The second caution is to remember that r explains the strength of linear
relationships. Look at the following example in Worksheet 2.1.6.
Worksheet 2.1.6
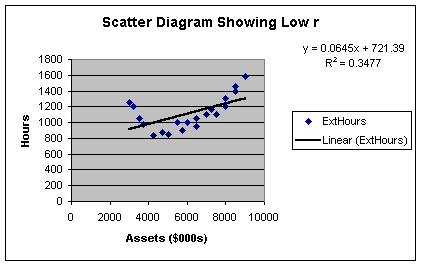
The R2 here is only 35%; meaning that client assets now only explain
35% of the sample variation in external hours. This gives an r of +0.59, which
borders on a weak relationship. In actuality, the relationship between client
assets and external hours is indeed strong - but the strength lies in the
curvilinear relationship between the two variables, not the linear
relationship. More on that in Module 3. For now, just recognize that many
people misapply the correlation coefficient to models that have curvilinear
rather than linear form.
A closing comment on correlation analysis. Since r is dimensionless and varies
between -1 and +1, it can be thought of as a standardized measure of the
strength of the linear relationship between two variables. Related to the
correlation coefficient is covariance, a non-standardized measure of the
strength of the linear relationship between two variables. The covariance is
computed by multiplying the correlation coefficient by the product of the
standard deviations of the two variables, thus mathematically defining the
relationship. While the correlation coefficient is the more commonly used
measure of the strength of the linear relationship between two variables,
financial models such as used in portfolio theory incorporate covariance so you
may see that statistic in a finance class.
Pause
and Reflect
Steps 1 - 3 of regression and correlation analysis give us information about
the form, direction and strength of the relationship between two variables. In
simple linear regression and correlation analysis, it is assumed that the two
variables are numerical and that the form of the relationship is a
straight-line. While these may seem simplistic assumptions, many relationships
in business and economics are modeled in this fashion.
This closes Module 2.1 Notes.
You should be able to get through Items 1 through 4 of Assignment 2 at this
point.
Outliers and Influential Variables
Before we go to Module Notes 2.2, let me illustrate one last caution in Steps 1
- 3 that you may run into as you prepare for Assignment 2. Recall that we
relied on the histogram in Module 1 to identify outliers to the distribution
under examination. We can also have outliers in regression analysis. Let's look
at a modified scatter diagram in Worksheet 2.1.7.
Worksheet 2.1.7
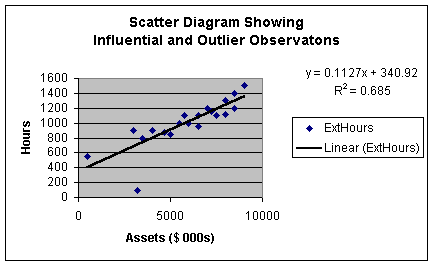
This scatter diagram is similar to that in Worksheets 2.1.2 and 2.1.5 except
that I changed the value of two of the observations. The observation with
assets of just over $3,000,000 and external hours of 100 is well below the
regression line. This would lead us to expect that it is an outlier to
the regression model. When we get to Module Notes 2.2, we will look at a way to
precisely determine if that observation is an outlier or not. We use the same
rules as before - if an observation is more than 3 standard deviations from the
regression line, it is an outlier.
There is one other observation that appears apart from the data. It is the observation
with a value of fewer than 600 external hours and less than $1,000,000 in
assets. While this observation is separated from the data, it is quite close to
the regression line. Thus, it is not an outlier to the regression model.
However, since the point is separated from the data, we call it an influential
observation. As in our study of descriptive statistics for individual variables
in Module 1, outliers and influential variables should be identified and
removed from the data set prior to numerical analysis. As before, sometimes
outliers and influential observations suggest a need to stratify the data
before further analysis; sometimes outliers and influential observations are
just individual events (sometimes even input errors!) that should be removed
before further analysis.
Reference:
Anderson,
D., Sweeney, D., & Williams, T. (2006). Essentials of Modern Business
Statistics with Microsoft Excel.
D.
Groebner, P. Shannon, P. Fry & K. Smith.
Business Statistics: A Decision Making Approach, Fifth Edition,
Prentice Hall. Chapter 14
Ken
Black. Business Statistics for Contemporary Decision Making. Fourth Edition,
Wiley. Chapter 13
| Return to Module Overview | Return to top of page |