CANOPY RESTRUCTURING IN RESPONSE TO HURRICANE DISTURBANCE
When chill November's surly blast Made field and forests bare Robert Burns Beasts did leap and birds did sing, Trees did grow and plants did spring Richard BarnfieldINTRODUCTION
One way to quantify recovery from disturbance is by measuring changes in the canopy structure as the forest canopy recovers. For the purposes of this study, canopy structure refers to the distribution of plant material through vertical layers above the ground, "the amount and organization of above ground plant material" (Norman & Campbell 1989), or one type of "complexity" as defined by August (1983). Canopy structure: influences the flow of air through the canopy and the flux of gases and radiation between the atmosphere and the forest; helps define the suite of microclimates available to other organisms living in or below the canopy (Norman & Campbell 1989, Welles 1990); is theorized to be positively correlated to available niches (MacArthur et al. 1962, Levins 1968), and therefore is proposed as one control on spatial patterns of biodiversity (Pianka 1966, Meffe & Carroll 1994). Forests with better developed and more diverse vertical structure have been associated with higher species diversity of: birds (MacArthur et al. 1962, Recher 1969, Wilson 1974, Moss 1978, Dickerson & Segelquist 1979, Elliot 1987), insects (Southwood et al. 1979), mammals (August 1983), and spiders (Greenstone 1984). In addition to the studies cited above, which measured canopy structure using foliage profiles, changes in canopy structure due to wind impacts have been quantified: directly by estimating canopy damage to stems (Frangi & Lugo 1991) or canopy damage to plots (Whitmore 1989), remotely by using aerial photography (Glitzenstein & Harcombe 1988), and indirectly using hemispheric photography (Turton 1992) or changes in solar radiation levels (Walker et al. 1992). Numerous authors have documented canopy restructuring following disturbance, but principally to calculate refoliation. Little work has been done to quantify changes in canopy structure through vertical layers of the canopy. Brokaw and Grear (1991) used foliage profiles to describe the impacts of Hurricane Hugo on the LEF, following the methodology established by Karr (1971) to relate habitat structure to bird population distributions, and Hubbell and Foster (1986) to examine treefall gap dynamics. Brokaw and Grear (1991) found that the hurricane had impacted the upper canopy levels most strongly, lowering the average canopy height by as much as 50%, and they predicted significant impacts on forest composition. Crow (1980) noted changes in the canopy stratification and height distribution of trees from 1946 (14 years after the last hurricane) and 1976. What is needed now is to study the closing of the canopy and the restructuring of canopy layers, particularly in the first decade of recovery. This study analyzes the dynamics of recovery of the canopy structure and the factors that influence these processes during the first five years of recovery. These efforts to predict patterns of vertical distribution of structure hold the promise of predicting, over time, the distribution of herpetofauna, avifauna, and invertebrates in the recovering forest (Reagen 1991, Waide 1991, Will 1991, Woolbright 1991, Wunderle 1992). I evaluate the role of two secondary gradients in influencing the dynamics of canopy restructuring: 1) community dynamics (quantified as API) and 2) topographic position. To examine the influence of community dynamics on the structure in the recovering canopy, I test the following hypothesis and three subhypotheses: Hypothesis 2 - Recovering forests have significantly different canopy structures when dominated by recruitment (early successional species) as opposed to dominated by regrowth (surviving late successional species). 2a. Maximum canopy height is significantly more variable in regrowing forest sites than in those dominated by recruitment of early successional species. 2b. Percent cover increases in each successive lower canopy interval in a regrowing forest. Maximum cover occurs at the lowest canopy interval - herb (0-1 m), through the first three years of recovery. 2c. By the third year after disturbance, forest sites dominated by recruitment have maximum cover at an intermediate canopy layer, therefore any lower layers have less vegetative cover. To examine the role of topographic position in influencing structure in the recovering canopy, I test the following hypothesis and two subhypotheses: Hypothesis 3 - Canopy structure is significantly different between sheltered valleys and exposed ridges. 3a. Independent of the recovery vector, valley sites have significantly lower percent cover in the lowest two canopy layers: shrub (1-4 m) and herb (0-1 m) than ridge sites. 3b. The difference between the lowest canopy layers is significantly greater in valley sites than in ridge sites when comparing regrowth to recruitment. That is, the shading effect of the canopy in a recruiting site is amplified in valleys.METHODS
Foliage profile data was collected at the 18 plots in the HRP, the 25 plots in the BEW (see Figure 22, Chapter 3), and an additional six plots in some of the least disturbed stands of the forest (referred to as controls). At each plot, nine samples were taken in a grid of three by three points, spaced 5 m apart (Figure 37). At each point, a 10 m extending pole was extended into the canopy. The pole was marked at ten unequal intervals of: 0 - 0.5 m, 0.5 - 1.0 m, 1.0 - 1.5 m, 1.5 - 2.0 m, 2.0 to 2.5 m, 2.5 - 3.0 m, 3.0 to 4.0 m, 4.0 - 6.0 m, 6.0 - 8.0 m, and 8.0 - 10.0 m. Five additional intervals of: 10 - 12 m, 12 - 15 m, 15 - 20 m, 20 - 25 m, and 25 - 30 m; were sampled by estimating height to foliage using a range finder. This gave a total of 15 canopy layers sampled. For each layer, any live vegetation touching the pole (or estimated to touch the pole if it was extended to the full 30 m) was recorded, an example of a 'semidirect method' for quantifying canopy structure (Norman & Campbell 1989). Each layer was recorded as having or not having vegetation touching the pole. Multiple contacts within a given interval were not recorded. This sampling methodology followed the protocol of foliage profile data collection established for the LEF by Brokaw and Grear (1991). Figure 37 - Foliage profile sampling methodology showing the nine sample points nested in the plot structure for the HRP and the BEW. I summarize foliage profile data by aggregating intervals (MacArthur et al. 1962, Karr 1971, Dickerson & Noble 1978, Hunter 1990) into five canopy layers, designated as: surviving 20-30 m, canopy 12-20 m, subcanopy 4-12, shrub 1-4 m, and herbaceous 0-1 m [similar to the four layers used by August (1983) except for the distinction between the 'surviving' former canopy and the new, lower, canopy]. Foliage profiles are constructed with percent cover, calculated by determining the percentage of points sampled with vegetation present, at each height interval (Karr 1971, Schemske & Brokaw 1981, Brokaw 1988, Brokaw & Grear 1991). At each height interval, the number of points at which vegetation was present is divided by the total number of points sampled. These percent cover values are plotted versus the height interval to create the profile (see Figure 38). Percent cover may be calculated by pooling all points in all plots, or by using the nine points in each plot as an independent sample and then calculating the mean and variance of all plots of a specific type, such as topographic position. Four additional summary measures of canopy structure were used. First, I calculated the average maximum canopy height by taking the mid-point of the highest interval with vegetation. Second, I calculated the Foliage Height Diversity (FHD) (MacArthur & MacArthur 1961) for each plot, using the five layers as 'species' and the count of touches in each layer as 'species counts', in the equation: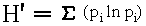
pi proportion of total touches that occur in
the canopy layer i
(Shannon & Weaver 1949)
Franreb and Ohmart (1978) state that the absolute amount of
vegetation may be of importance, rather than its distribution.
For the third summary measure I calculated foliage density by
taking the total number of vegetation touches (at all levels)
and dividing by the total number possible in a plot. Each plot
has nine points that are sampled at five layers giving 45
possible points. Foliage density is expressed as a percent,
and is numerically equivalent to averaging the percent cover at
all levels.
For the final summary measure of canopy structure I used
the original 15 layer data set and counted the total number of
touches at each sampling point as an estimate of leaf area
index (LAI). LAI represents the leaf surface area per unit of
forest floor, or the number of layers of leaves above any point
on the forest floor. Since multiple touches in a given layer
were ignored, this estimate of LAI should be consistently low,
but can still be used to compare between plots. The LAI is
averaged for each plot using the nine sampling points.
A variety of statistical tests have been applied to
foliage profile data and several are used in this study.
Comparison of the resulting interval patterns is accomplished
by using t-tests for individual levels, one-way ANOVA for
testing for differences between all layers; and 2 x 5
contingency tables, Wilcoxin two-sample test (Brokaw & Grear
1991), Kolmogorov-Smirnov Test (Brokaw 1988) and calculation of
foliage diversity for comparing the overall patterns of foliage
distribution between two categories of plots (MacArthur &
MacArthur 1961), such as ridge versus valley plots.
Three of these methods were used to test for significant
canopy structure differences between plots with different
recovery vectors, as defined by API values (Hypothesis 2). For
each recovery vector, the H' values, foliage density and LAI
were averaged then tested for significant differences using a
t-test. The pattern of foliage distribution, the foliage
profile, is tested for significant difference using a 2 x 5
contingency table (Aber 1979) and calculated G-test value
(Sokal & Rohlf 1981). To test for difference in the median
value of the foliage profile, the Wilcoxin two-sample test was
applied (Brokaw & Grear 1991). The foliage profile can also be
viewed as a frequency distribution and two distributions can be
compared using the Kolmogorov-Smirnov test for goodness of fit
(Brokaw 1988).
To examine Hypothesis 2A, I tested for significant
difference in the variance of canopy height between plots
following different recovery vectors, using Bartlett's test of
homogeneity of variances (Sokal & Rohlf 1981). To examine
differences between layers (Hypotheses 2B and 2C) I used a one-
way ANOVA (Hale 1992) and t-tests between specific layers.
I used the same three methods to test for significant
canopy structure differences between plots in different
topographic position, specifically ridges and valleys
(Hypothesis 3), as used to test Hypothesis 2. A t-test was
used to test for differences in the lower two canopy levels
(Hypothesis 3A). And, to test for significantly greater
differences in valley sites, I applied a two-way ANOVA for each
of the lower two canopy layers, categorizing the data by API
value and topographic position, and testing for significant
interaction between the categories (Sokal & Rohlf 1981).
RESULTS
Both community composition, as differentiated by API values, and topographic position influence the vertical structure of the recovering canopy. The API, topographic position, percent cover in each of the five layers, canopy height, FHD, and foliage density are reported for all 43 plots in Appendix C-XVI and summarized in Table 18. The foliage profile for HRP and BEW is presented in Figure 38, both as the original 15 layers of data (Figure 38A), and the data collapsed into five layers (Figure 38B). Combining the data into five layers emphasizes the differences between the two sampling sites. The BEW has greater percent cover in the subcanopy layer which may reflect its higher API (1.71). This site was exposed to more intense hurricane wind (Scatena & Larsen 1991) and is now dominated by a subcanopy layer of Cecropia schreberiana which had not reached the canopy (12-20 m) layer and is shading out the lower levels of vegetation. The HRP, with a lower API (1.38), has greater percent cover in the canopy layer and the shrub layer. A more direct examination of Hypothesis 2 is presented in Figure 39, comparing the foliage profile data combined into five layers and separated into the plots with API < 1.33 and plots with API > 1.33. Figure 39A graphs all 43 plots. As was the case between sites, plots with higher API have a greater percent cover in the subcanopy layer. Plots with a lower API have greater percent cover in the shrub and canopy layers, and also in the surviving layer. To examine if these differences might be related to the difference between sites rather than API values (BEW is predominately API > 1.33, HRP is evenly split), Figure 39B show the distribution of percent cover for only the HRP plots. Here the plots with API > 1.33 have less cover in the subcanopy layer and greater percent cover in the shrub layer. The re-establishing canopy of early successional species may not have yet reached the subcanopy layer in the plots on the HRP. When these two profiles (API < 1.33 and API > 1.33 for all 43 plots) are tested, only one of the several tests applied indicated a significant difference. The contingency table analysis yielded an adjusted G-value of 4.02 (p>0.05). For the Wilcoxin two-sample test, C=13 (U0.05=21). The Kolmogorov- Smirnov Test yielded D=0.0211 (D0.05=0.092; n1=795, n2=303). To investigate the possibility of topographic interference in identifying significant differences between these two groups of plots, the ridge plots (D=0.066, D0.05=0.209, n1=170, n2=56) and valley plots (D=0.050, D0.05=0.16, n1=125, n2=120) were tested separately, but no significant difference was found (Figure 40). Table 18 - Summary of measures of canopy structure for different categories of plotsNumber of Percent Cover by Layer Average Foliage Category Plots Herb Shrub Subcanopy Canopy Surv Height H' Density LAI
SITE
HRP 18 75.31 91.36 69.14 42.49 8.64 13.53 1.36 57.41 4.78 BEW 25 74.22 84.45 85.33 28.00 9.33 12.22 1.33 55.47 5.24 Controls 6 70.37 59.26 88.89 83.33 18.52 19.52 1.45 64.09 5.31
TOPOGRAPHY
Valley 10 73.74 78.89 88.89 21.11 10.00 12.22 1.30 54.44 4.82 Bench 4 83.34 100.00 58.34 50.00 2.78 12.54 1.30 58.89 4.58 Slope 21 76.72 86.77 80.42 37.56 11.11 13.41 1.37 57.57 5.27 Ridge 8 66.67 93.06 70.84 33.33 5.56 11.90 1.36 53.89 4.93
COMMUNITY
API < 1.33 12 73.15 87.04 78.71 37.04 10.75 12.87 1.33 57.34 4.90 API > 1.33 31 75.27 78.50 87.46 32.97 4.63 12.51 1.35 55.77 5.20
Totals 49 74.15 83.90 79.82 40.13 10.20 13.60 1.36 57.24 5.06
Figure 38 - Foliage profile data for all 15 layers of canopy sampled (A) and for this data combined into five canopy layers (B). Comparing Hurricane Recovery Plot (HRP) and Bisley Experimental Watershed (BEW). Figure 39 - Foliage profiles comparing plots with API < 1.33 to those with API > 1.33. Data compressed into five layers. A. data for all 43 plots from both the Bisley Experimental Watershed and the Hurricane Recovery Plot (n=387). B. Data form only the Hurricane Recovery Plot (n=162) Figure 40 - Foliage profiles combined into five layers, comparing plots with different API and separated by topographic position. A. valley plots. B. ridge plots. Figure 41 - Histogram of maximum canopy heights comparing plots with API < 1.33 and plots with API > 1.33. Canopy heights combined into intervals of 5 m and percent of sampling points with a maximum height in each interval is given. Finally, examining the summary indices, the average H' values between the two groups of sites yielded a t-value=1.328 (df=41, p>0.05). The foliage density was not significantly different between plots (t-value=0.117, p>0.05). However, LAI was significantly lower in the plots with API < 1.33 (mean 4.66) than in plots with API > 1.33 (mean=5.20, t-value=2.267, p<0.05). This may reflect the finer resolution of canopy sampling in the lower layers, where vegetation is expected to be concentrated in plots dominated by recruitment. Figure 41 is a graphic representation of the data pertaining to Hypothesis 2A, examining if the two groups of plots are significantly different in the variation of their maximum canopy heights. The number of sampling points whose maximum canopy height falls into each 5 m interval is tallied. For example, both groups of plots have 10 to 15 percent of the sampling points with a maximum canopy height of less than 5 meters. The two distributions are clearly different, with canopy concentrated in the 20-25 m interval for plots with API < 1.33, and canopy concentrated in the 10-15 m intervals for plots with API > 1.33. However, testing for homogeneity of variances, yielded no evidence of a significant difference (chi2=1.123, p>0.05). To determine if plots with API < 1.33 have increasing percent cover in each layer down through the canopy, the percent cover for each layer was plotted (Figure 39) and the distribution was tested using a one-way ANOVA. The ANOVA indicated significant differences between layers (F=58.46, P<0.001), but the lowest layer (herb) does not have the highest percent cover. To determine if plots with API > 1.33 have the largest percent cover in the subcanopy layer, the percent cover for each layer was plotted (Figure 39) and again the percent cover for each layer was tested using a one-way ANOVA. The ANOVA indicated significant differences between layers (F=110.38, P<0.001). Individual t-tests were applied between the subcanopy layer and the shrub and herb layers. Both the herb layer and the shrub layer had significantly less cover than the subcanopy layer (t=3.723, p<0.001; and t=1.809, p<0.05). To examine the influence of topographic position on canopy structure, the foliage profiles were plotted for the combined five layers and separated into the most extreme topographic classes, ridges and valleys (Figure 42). The pattern of the foliage profile for ridge plots is similar to that for the plots with API < 1.33. The ridge plots have increasing percent cover with each interval lower into the canopy, except for the herb layer where the percent cover decreases. The valley plots have a foliage profile similar to plots with API > 1.33, with a maximum percent cover in the subcanopy layer. When these two profiles were tested, no significant difference was detected. Comparing the average H' values between the two groups of sites yielded a t-value=1.054 (df=17, p>0.05). Comparing foliage density (t-value=0.219, p>0.05) and LAI (t-value=0.298, p>0.05) also showed no significant differences. The contingency table analysis yielded an adjust G-value of 5.97 (p>0.05). For the Wilcoxin two-sample test, C=14 (U0.05=21). Finally, the Kolmogorov-Smirnov test yielded D=0.66 (D0.05=0.125; n1=226, n2=245). To investigate the possibility of interference from variation in the API values of the plots in each topographic position in identifying significant differences between these two groups of plots, the plots with low (<1.33) API (D=0.096, D0.05=0.219, n1=170, n2=56) and the plots with high (> 1.33) API (D=0.077, D0.05=0.16, n1=170, n2=125) were tested separately, but no significant difference was found. Figure 42 - Foliage profiles comparing plots from different topographic positions. Data compressed into five layers. To examine Hypothesis 3a, whether valley sites have lower percent cover in the herb and shrub layers than ridges have in the herb and shrub layers, a t-test was applied to each level, comparing the ridge and valley sites. The herb layer was not significantly different between the two topographic positions (t=0.670, p>0.05). The shrub layer has significantly lower percent cover in the valley sites (t=3.12, p<0.001). To examine the interaction between topography and the restriction of growth relative to recovery vectors defined by API, an ANOVA was applied to the plots categorized by API and topography (Table 19). The difference between the shrub layer counts in valley sites is greater than the difference between sites on ridges (1.0 and 0.21 respectively), but this difference is not significant (F=0.72, p>0.05). The herb layer shows no such trend, and has greater cover in plots with API > 1.33, in both ridges and valleys (Table 19). Table 19 - Influence of topography and community dynamics on structure in the understory. Mean and standard deviation (SD) of counts of vegetation touches in the lower two canopy layers of plots categorized by API value and topographic position. Plots from both BEW and HRP.
Shrub Layer Herb Layer API Topography N mean SD mean SD
>1.33 Valley 5 6.60 1.14 7.20 1.30 <1.33 Valley 5 7.60 0.89 6.00 1.58 >1.33 Ridge 7 8.29 0.76 6.14 1.07 <1.33 Ridge 2 8.50 0.71 5.50 0.71
DISCUSSION
Forest canopy structure differs between the recovery vectors because of the difference in severity of damage and the resulting vertical gradients of abiotic factors, principally solar radiation. Regrowing forest stands have surviving stems that result in a variable upper canopy surface that allows some solar radiation to penetrate through to the lower canopy layers. A forest stand dominated by recruitment occurs where more severe disturbance results in initially higher levels of solar radiation at the forest floor. However, as a pulse of new trees is established, the resulting canopy is both even and dense; allowing less solar radiation to penetrate to lower levels as the canopy grows upward. The difference in solar radiation available to lower canopy levels is amplified by topographic position and topography influences the severity of damage from wind. Therefore topographic position also influences forest canopy structure. Sheltered valleys receive less solar radiation due to shading of the terrain, so the lower canopy levels have less structure and the difference between these two vectors of recovery is increased. More diffuse solar radiation penetrates to the lower canopy levels on exposed ridges, so the vegetation structure at these levels is denser and the difference between the two vectors of recovery is diminished, although this difference was not significant in this study. The herb layer did not follow expected trends. In plots dominated by regrowth (API < 1.33) I predicted the herb layer would have the highest cover, but this layer had less cover than the shrub layer. This could be the result of shading from the shrub layer. If solar radiation is influencing the foliage structure in the herb layer, we would expect a lower percentage cover in valleys where lateral solar radiation is restricted. This was not the case, as percent cover was higher in the herb layer of valley sites compared to the herb layer of ridge sites. Possibly structure is influenced also by a soil moisture gradient. Figure 43 - Projected patterns of recovery of canopy structure. Two vectors of recovery based on API, A. plots with API < 1.33, B. plots with API > 1.33. Pre-hurricane levels based on data from Brokaw and Grear (1991). Tree community composition, quantified as API, can be used to extrapolate canopy structure through the recovery phase. If we use Brokaw and Grear's (1991) pre-hurricane structural measurements as an assumed endpoint to recovery, we can predict two distinct paths to this endpoint. In plots with API < 1.33, the upper two layers of the canopy will continue to grow outward, while the lower two layers decrease in percent cover due to the restricted solar radiation environment (Figure 43A). In plots with API > 1.33, the percent cover decreases in the three lower levels as the canopy moves upward first to the canopy (12-20 m) layer, then finally to the highest level (20- 30 m) (Figure 43B). Weaver (1989) predicts three stages to recovery from hurricane disturbance in the LEF: 1) colonization and growth, 2) building, and 3) maturity. His data indicates a shift from the first to the second stage at 20 years. Crow (1980) found that stem number approaches steady state after 44 years of recovery from the 1932 hurricane, so I assumed 40 years to complete canopy recovery. Figure 44 - Comparison of two foliage profiles with similar FHD. Distribution is plotted as a continuous profile, with foliage density at each level. (after MacArthur & MacArthur 1961). FHD has been a common way to quantify canopy structure, but it may not be appropriate for distinguishing between foliage profiles. Foliage profiles may have very different shapes but similar values for H', as indicated by two examples from MacArthur and MacArthur (1961) (Figure 44). In this example both profiles are not even, but have one or more areas of higher concentration of structure. When the research question is concerned with the location of dense vegetation, another method must be used to distinguish between distributions. Karr and Freemark (1983) use the Wilcoxin matched-pairs signed-rank test, which seems to be sensitive to differences when all or most of the canopy layers are lower in one profile than in another, such as is the case in comparing pre- and post-disturbance profiles. However, when the profiles differ by location of concentration of vegetation, as is the case in comparing the vectors of recovery in this study, this test does not detect differences. The Wilcoxin matched-pairs signed-rank test sums positive and negative differences. These differences will tend to cancel out when one profile is larger in one layer but smaller in another. The Kolmogorov-Smirnov test, suggested by Brokaw (1988), utilizes the largest difference between foliage in any one layer, and therefore can detect when one layer has a much higher concentration in one profile. But, the test ignores cumulative differences in other layers. A contingency table, as used by Aber (1979), seems the most appropriate test for detecting large differences in a single layer or smaller differences in several layers which cumulatively can indicate a significant difference between two foliage profiles. Yet, even this test indicates no significant difference between foliage profiles which appear distinctly different (e.g., Figures 39 and 42). Though the question of appropriate statistical tests remains unanswered, clearly topography and tree community dynamics influence vertical structure of the canopy of a forest recovering from hurricane disturbance. Pianka (1966) stated that relating animal species diversity to canopy diversity only changes the focus to factors that control canopy diversity. This study indicates that intensity of damage, reflected in differing vectors of recovery, influences canopy structure. This influence is mitigated by topography. Although the mechanism of control is probably a gradient of solar radiation and possibly soil moisture, these descriptive relationships to damage severity and topography allow the simulation of patterns fo canopy restructuring, over the landscape, following hurricane disturbance.Return to the Table of Contents