FACTORS INFLUENCING THE SPATIAL PATTERN OF HURRICANE DAMAGE
All nature is but art unknown to thee; All chance, direction which thou canst not see; All discord, harmony not understood; All partial evil, universal good; Alexander PopeINTRODUCTION
A critical concern in the analysis of the impacts of catastrophic winds on forests is the spatial pattern of the damage, and the factors that influence this pattern (Wiley 1965, Shaw 1983, Foster 1988b, Putz & Sharitz 1991, Bellingham et al. 1992, Foster & Boose 1992, Boose et al. 1994, Everham 1995). The size-frequency distribution associated with a given disturbance regime may influence the life histories of recovering tree species (specifically regeneration requirements and strategies), pattern of species diversity following a given disturbance, and the likelihood of a competitive equilibrium resulting from a mosaic of patches (Denslow 1980). Patch size influences the dynamics of tropical and temperate forest recovery (Hartshorn 1978, Runkle 1981, 1984, 1985; Brokaw 1985a,b), regardless of the cause of patch creation. Specifically for catastrophic wind events, recovery in larger patches is dominated by recruitment of early successional species, whereas smaller patches often recover through sprouting and regrowth of species previously established (Dunn et al. 1983, Webb 1986, Putz & Brokaw 1989). The proportion of species adapted to large, as opposed to small, patches of disturbance is related to the frequency of occurrence of these patch sizes. If a given community has developed in a regime of large patch-size disturbance, a large proportion of species would exhibit life histories that require such patches for regeneration, and overall species diversity should decrease in time following a large-scale disturbance (Denslow 1980). The application of the terms "large-scale" and "catastrophic" are both ambiguous in relation to wind disturbances. Although some wind disturbances, for example hurricanes or cyclonic storms, may impact hundreds of square kilometers (Dunn & Miller 1960), it is incorrect to infer homogeneously severe disturbance throughout the entire region. In reality, the severity of damage varies at both large (kilometers) and small (tens of meters) spatial scales. Heterogeneity in wind damage has been observed over the landscape (Boose et al. 1992, Foster & Boose 1992, Walker et al. 1992) and at smaller spatial scales (Conrad 1945, Browne 1949, Stoeckeler & Arbogast 1955, Webb 1958, Wiley 1965, Foster 1988b, Glitzenstien & Harcombe 1988, Putz & Sharitz 1991, Bellingham et al. 1992, Foster & Boose 1992, Walker et al. 1992, Boose et al. 1994). Patch sizes for wind damage in these 'catastrophic wind disturbances' have been reported to be as low as 20 m2 (Webb 1986), 30 m2 (Foster 1988b), and 0.04 ha (Foster & Boose 1992). A variety of factors have been proposed to influence patterns of wind damage in forests including: stem size, stand conditions, species differences, tree pathogens, topography, soil conditions, and previous wind damage (Bromley 1939, Smith 1946, Stoeckeler & Arbogast 1955, Neustein 1971, Putz & Sharitz 1991, Allen 1992). The factors that influence the severity of damage can be separated conveniently into those that are biotic versus abiotic factors. It has been suggested that the importance of different factors in controlling the severity of wind damage varies with shifts in spatial scale (Foster 1988, Lawrence et al. 1991, Boose et al. 1994). At the landscape scale, abiotic factors such as topography and storm intensity are most important (Fetherston 1987; Foster 1988). Foster (1988) states that at the scale of a forest stand, the vegetation (structure and species' susceptibility) and the factors that control vegetation (e.g. previous disturbance) control the severity of damage. Understanding the factors that control patterns of damage are important to mitigating damage and managing forest resources in areas prone to wind disturbance. In addition, these factors control patterns of damage and recovery of natural forests in these areas and lead us to a better understanding of long-term forest dynamics. The measurements that have been used to quantify the severity of disturbance are not standardized (Everham 1995) and this leads to difficulty when different wind disturbance events are compared (Lugo et al. 1983, Glitzenstein & Harcombe 1988, Ackerman et al. 1991, Scatena & Larsen 1991). Of the 48 papers reviewed in Everham (1995) that included quantification of damage severity, 28 different methodologies were applied. These different measures of damage have resulted in different conclusions regarding: patch-size distribution, spatial pattern of damage, and factors that influence this pattern. To summarize, the size of a disturbed patch influences recovery, and the pattern of patches over the landscape may affect the life histories of the affected communities. Both patch size and pattern of patches vary depending on the measure used to quantify disturbance. Understanding the factors that control patterns of damage may help in the management of forest resources in hurricane-prone areas and in understanding the long-term forest dynamics in these areas. Following Hurricane Hugo we established a 16 ha plot in the Luquillo Experiment Forest, Puerto Rico. One advantage of a large, contiguous plot is the ability of examining spatial patterns over the landscape. Therefore, I investigate three questions: 1) Do observed spatial patterns of hurricane damage vary when different measures of damage are used? 2) What is the patch structure of hurricane damage?, and 3) What are the relative roles of abiotic and biotic factors in influencing patterns of hurricane disturbance?STUDY SITE
This portion of my research was conducted near the El Verde Field Station (18o20'N, 65o49'W). This area is classified as subtropical wet forest in the Holdridge System (Ewel & Whitmore 1973). The forest is named for the tabonuco (Dacryodes excelsa Vahl. BURSEACEAE) tree, and is the lowest (200 - 600 m a.s.l.) of four vegetation zones occurring along an elevational gradient in the LEF. In addition to tabonuco, the forest in the area includes, Prestoea montana (R. Grah.) Nichols ARECACEAE, and trees Manilkara bidentata SAPOTACEAE (A. DC.) Chev. and Sloanea berteriana Choisy ELAEOCARPACEAE (Odum & Pigeon 1970, Brown et al. 1983). The general topography is mountainous with northwest-running drainages. Soils in the area are mostly zarzal clay, which are deep oxisols of volcanic origin (Huffaker in press). Rainfall at the station averages ca. 350 cm per year (Brown et al. 1983). Starting nine months after Hurricane Hugo a 16-hectare plot was established following the methodology established by Hubbell and Foster on Barro Colorado Island, Panama (Hubbell & Foster 1983, 1985). The Hurricane Recovery Plot (HRP) is 320 m by 500 m and cuts through two watersheds (see Figure 7 in Introduction and Overview). The southern portion of the Hurricane Recovery Plot is similar to virgin stands of tabonuco forest (Odum 1970a). However, due to human disturbance, none of the plot can be considered to contain primary forest. Forests in the El Verde area were subject to stand improvement cutting in 1937 and 1946. Between 1944 and 1953, additional timber harvest removed approximately one-half the volume of tabonuco (Odum 1970a). The northern portion of the plot was subject to clear cutting or unidentified agricultural practices prior to 1934 (D. Garcia-Montiel, personal communication). A 1936 aerial photo of the area indicated much of the northern portion of the plot had forest cover of 20 - 80% (M. Fluet, personal communication). This area of the plot now supports secondary forest, whose canopy is primarily Casearia arborea (L.C. Rich) Urban FLACOURTIACEAE. The difference between the northern and southern regions of the HRP is demonstrated clearly with maps of the distribution of Dacryodes excelsa and Casearia arborea (Figure 14). Figure 14 - Distribution of Dacryodes excelsa and Casearia arborea in the Hurricane Recovery Plot. All stems >10 cm dbh are mapped.METHODS
Over the 16 ha of the HRP, a grid of points was surveyed at 20 m intervals. Within each 20 m by 20 m quadrat, 16 additional points were placed at 5 m intervals. This grid structure allows multiple spatial resolutions of the patterns of damage. In this chapter I investigate patterns using the: 1) finest resolution, of 6400 5 m by 5 m subquadrats, 2) data combined into 1600 10 m by 10 m subquadrats, and 3) data combined into 400 20 m by 20 m quadrats. I used the surveyed elevation data to determine average elevation, aspect, and slope for each quadrat or subquadrat. Aspect was then aggregated into five categories of exposure relative to the predominately northeast hurricane winds (4: northeast, 3: east and north, 2: northwest and southeast, 1: west and south, 0: southwest). I then used the digital elevation model derived from the elevation data to categorize each quadrat or subquadrat as: 1) ridge, 2) valley, 3) bench (a slope of < 15%), or 4) slope (> 15%). Aerial photos from 1936 were used to categorize cover class and presence of gaps at that time. Regions of the plot were characterized as < 20%, 20-50%, 50-80%, or > 80% percent cover for 1936, and each quadrat was scored as gap or non-gap (M. Fluet, personal communication). Each quadrat or subquadrat was described in terms of soil type and rockiness (Mount et al. 1994). These eight variables collectively were grouped as abiotic factors. Each tree 10 cm in diameter or greater was identified, tagged, measured for diameter at 1.3 m above the ground (dbh), mapped, and assessed for hurricane damage. I describe each quadrat or subquadrat in terms of 14 biotic variables, specifically: total number of stems, basal area, and abundance of each of twelve tree species (Appendix C - VI). Finally, I quantified hurricane damage in five ways. First, by five mutually exclusive stem damage categories, each examined as counts of: 1) stems snapped off above ground, 2) stems uprooted, 3) stems broken at the ground but not uprooted, 4) stems bent by the wind or by other treefalls, and 5) stems that did not recieve any of the previous four types of damage, but did have damage to branches 10 cm or larger in diameter. Second, damage was quantified as counts of stem mortality per quadrat or subquadrat. Third, damage was expressed per quadrat or subquadrat, by calculating loss of basal area combining all stems either damaged or killed. Fourth, counts of total number of stems damaged (combining snapped, uprooted, broken at the ground, or bent), mortality, and basal area damaged, were converted to proportions of the total per quadrat or subquadrat. Fifth, damage was measured as the post-hurricane canopy height, assessed at each of the 6400 5 m subquadrat grid points from April to July of 1992 (19 - 22 months after the hurricane) and compared to the assumed per-hurricane height of 30 m. The result is 12 damage variables (Appendix C-VI). To investigate the changes in spatial pattern resulting from different measures of damage, I developed hurricane damage maps using each measure of damage (root broken and bent stems were not analyzed because of their low frequency). The range of severity of damage (minimum to maximum) was divided into five equal categories and each quadrat or subquadrat was scored (1: least impacted, to 5: most damaged). Three techniques were used to compare the resulting spatial patterns. The simplest method of comparison of spatial pattern is to overlay two maps and record the proportion of cells that are the same on both maps. However, this comparison is dependant on the spatial resolution of the maps. Turner et al. (1989) describe the multiple resolution goodness-of-fit technique, where the fit (Fw), the proportion that match, is calculated for spatial resolutions from one grid cell up to the maximum possible for the map. That is, the 'fit' is calculated for the finest spatial resolution, then grid cells are combined and averaged at progressively larger sizes until the total average for one map is compared to the total average for the other. The average of all spatial scales (Ft) is then calculated. I report Fw for a spatial scale of one grid cell (comparing the maps at the 5m-by-5m subquadrat scale), and Ft. These two measures determine proportion correctly matched, but since the calculation is based on matching or not matching, this technique fails to quantify the degree of error in maps with more than two categories. In multi-category maps, a comparison between two maps cells that differ by a value of one and two map cells that differ by a value of three both score as non- matched. To measure the degree of difference, the above calculations were modified to measure average difference (FD) between maps. Average difference is calculated: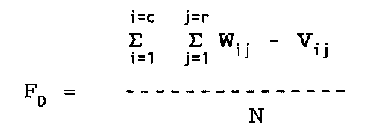
W - value for first map grid cell
V - value for second map grid cell
i - x coordinate for grid cell (column)
j - y coordinate for grid cell (row)
c - total number of columns
r - total number of rows
N - total number of grid cells (c * r)
Calculating FD accounts for the degree of difference in
mismatched cells when a map has more than two categories, as in
the case with the comparisons in this study.
Next, these maps were used to generate the frequency
distributions of patch sizes. In this case, a patch is defined
as adjacent grid cells with equally severe damage. Categories
4 and 5 of each measure of damage were considered severe and
used to define a damaged patch.
Since data were collected over a gridded plot, both
quadrat variance models (using quadrat or subquadrat data) and
distance models (using grid points) are applicable for examining
spatial patterns. I use the T-square Index of Spatial
Pattern (C) and the Distance Index of Dispersion (I) to determine
whether damage was clumped, regularly, or randomly
distributed (Ludwig & Reynolds 1988). Both compare distances
to individuals, in this case damaged trees, to expected
distances in a population that is randomly distributed over a
landscape. I used only the inner 286 grid points as data for
the analysis to minimize the effects of the plot edge. The T-
Square Index of spatial pattern has a value of 0.5 for random
spatial patterns. Values less than 0.5 indicate a regular
distribution; more than 0.5, a clumped distribution. The
Distance Index of Dispersion has a value of 2 for a uniform
pattern. Values of less than 2 indicate a uniform pattern;
more than 2, a clumped distribution. Both techniques allow
calculation of a z value to test for significance.
Quadrat variance methods were applied to five randomly
selected transects through the data to test for significant
patch spacing. These 500 m transects used the finest
resolution of subquadrat data, 100 5 m by 5 m subquadrats.
Each of the twelve measures of hurricane damage are examined
for spatial pattern of patches of damage. As recommended by
Ludwig and Reynolds (1988), maximum spacing size examined was
10 grid cells (N/10). Three of the transects are analyzed
using Paired Quadrat Variance (PQV) and Blocked Quadrat
Variance (BQV), to explore for possible patterns. The observed
patterns are tested for significance in the remaining two
randomly selected transects using the Random Paired Quadrat
Technique (Ludwig & Reynolds 1988).
I applied principal component analysis (PCA) for
exploratory data analysis, in an attempt to identify trends in
the data set. The goal of PCA is to reduce a complex data set
into a smaller number of uncorrelated indices that account for
the majority of the variance of the data (Manly 1986) and thus
is appropriate in attempting to summarize a mass of data such
as the HRP data set (Johnson & Wichern 1988). The analysis was
run for: 1) all variables, abiotic, biotic, and damage, 2)
damage variables only, and 3) for all variables and including
the coordinates of the grid cell to incorporate information on
the location of each plot.
To examine the relative roles of abiotic and biotic
factors in influencing damage, I applied canonical correlation
analysis (CCA). The goal of CCA is to identify and quantify
the association between two sets of data (Manly 1986, Johnson &
Wichern 1988). As in PCA, each data set is reduced to summary
canonical variables, and the canonical correlation measures the
strength of association between the two sets of variables.
This analysis was done with the damage variables (all 12) as
one set of variables and then varying the data used as the
second set of variables in four ways, using: 1) only the eight
abiotic variables with additional dummy variables to account
for categorical data , 2) only the 14 biotic variables, 3) all
22 biotic and abiotic variables with the dummy abiotic
variables included (there are no categorical biotic variables),
and 4) sorted by the categorical variables of topography, cover
classes, and soil. Both PCA and CCA were run at three spatial
scales, using the: 400 20 m by 20 m grid cells (20 m scale),
1600 10 m by 10 m grid cells (10 m scale), and 6400 5 m by 5 m
grid cells (5 m scale).
The use of dummy variables is recommended to account for
categorical variables in both PCA and CCA, which are based on
models of linear association (Jongman et al. 1987). For
example, if variable A has three values, two new variables, A1
and A2, are created. These three variables are used to
represent the categorical data: A value of 1 is represented by
A = 1, A1 = 0, and A2 = 0. A value of 2 is represented by A =
0, A1 = 1, and A2 = 0. A value of 3 is represented by A = 0,
A1 = 0, and A2 = 1. This technique is applied to: topography,
1936 forest cover, 1936 forest gaps, soil type, and substrate.
Another approach to account for nonlinear relationships of
categorical data is to run the analyses separately for each
categorical variable. This approach was used only for the 1936
cover classes, topographic classes, and soil types.
RESULTS
A total of 13,078 live stems of 88 tree species were assessed for damage; 16.7% had stem damage and an additional 15.4% received major branch damage (Zimmerman et al. 1994). Hurricane induced mortality was 9.0%, 30 months after the passage of Hugo. Overall, 18.6% of the basal area was damaged (counting stems damaged or killed). Table 10 presents a summary of the data used in the analyses. The summary of results for biotic and damage variables varies slightly from those above, as the analysis used only 12 of the 88 species, which included 74.8% of all stems examined. Figure 15 shows the results of using different measures of damage to quantify spatial patterns of damage. These maps of pattern of damage are based on branch damage, mortality, stem damage and basal area lost. All data are presented at a 5 m spatial scale viewed from the northwest, looking upslope. In all four maps the dark areas indicate most severe damage. Branch damage shows the strongest landscape pattern, with damage concentrated in the southern half of the grid. Stem damage and mortality shows an opposite, but weaker trend, with higher stem damage and mortality in the north half of the grid. Percent basal area shows a similar trend. At finer resolution, all four measures of damage show different spatial patterns. To quantify the differences in the patterns generated by these different measures of damage, each pair of maps was overlaid and the "fit" between the maps was calculated (Table 11). The upper right half of Table 11 presents the measured fit for a spatial resolution of 5 m by 5 m subquadrats (F1) over the average fit for all spatial resolutions (Ft). The lower half of the table presents the average difference between grid cell values (FD), with no shift in resolution. Note that in the upper half of the table, a higher value represents a better 'fit' and in the lower half of the table higher values are related to greater differences and poor fit. All three measures seem to capture the same characteristics of similarity and difference between maps. Plotting F1 versus Ft results in a positive linear relationship with a slope of 1.002 (p<0.005) and an r2 value of 0.897. Plotting F1 and Ft versus FD results in r2 values of 0.947 and 0.941, respectively. Table 10 - Summary of results for Hurricane Recovery Plot variables, using the 5 m by 5m subquadrat scale. See Appendix C-VI for units.ABIOTIC VARIABLES: categories average minimum maximum 5 4 3 2 1 0 Elevation - 378.1 333.6 428.2 Exposurea - 1237 2145 1769 884 Slope - 25.4 0.00 108.9 Topographyb- 356 3252 1770 1022 1936 Coverc- 2172 2283 1531 414 1936 Gapsd - 708 5692 Soil Typee - 184 4009 350 1823 34 Substratef - 350 1919 3640 491
BIOTIC VARIABLESg: total average maximum Stems - 12914 2.02 10 Basal Area - 5787427 904.29 18914.8 PREMON - 4414 0.69 7 CASARB - 1073 0.17 5 DACEXC - 1030 0.16 7 MANBID - 665 0.10 5 INGLAU - 549 0.09 3 SLOBER - 501 0.08 3 TABHET - 333 0.05 4 GUAGUI - 315 0.05 3 MATDOM - 254 0.04 4 ALCLAT - 205 0.03 3 DIDMOR - 196 0.03 2 CECSCH - 130 0.02 3
DAMAGE VARIABLESg: total average maximum Snapped - 912 0.14 3 Root - 162 0.03 3 Tip-up - 853 0.13 4 Bent - 92 0.01 2 Branch - 2007 0.31 7 Dead - 1077 0.17 4 % Dead - 7. 100 Total Stem - 2160 0.34 5 % Stems - 14. 100 BA Damaged - 1078463 168.5 10568.3 % BA - 16. 100 Height - 14.16 30
a Aspect exposure categories: 4 - NE, 3 - E or N, 2 - NW or SE; 1 - W or S; 0 - SW; b Topography: 4 - ridge, 3 - slope, 2 - bench, 1 - valley; c Percent cover (1936): 4 - 80-100%, 3 - 50-80%, 2 - 20- 50%, 1 - < 20%; d Gaps (1936): 1 - gap, 0 - no gap; e Soil type: 5: fluvaquent, 4: zarzal clay, 3: prieto clay, 2: cristal clay, 1 - coloso clay; f Substrate: 4: very rubbly, 3: very bouldery, 2: rubbly, 1: extremely bouldery; g all minimums are zero Figure 15 - Spatial patterns of hurricane damage to the 16 ha Hurricane Recovery Plot using four different measures of damage: A. basal area damaged, B. branch damage, C. mortality, D. canopy height decrease. View from the northwest. Maps use the 5 m grid cell resolution. Dark regions indicate areas with the most severe damage. Figure 16 - Change in Fit between maps of different measures of hurricane damage, with shifting spatial scale. Six comparisons representing the range of FD values. Fit was calculated as average difference (FD) values for corresponding grid cells on two maps, with grid cells of 20 x 20 m, 10 x 10 m, or 5 x 5 m. Damage is measured as basal area lost (BA), canopy damage (Height), percent of stems damaged (% Stems), number of stems with branch damage (Branch), percent of stems killed (% Dead) and number of stems uprooted (Tip-up). The best fit (and therefore lowest difference) occurs when comparing measures such as number of stems dead to percent stems dead (Ft=0.91, FD=0.16). The largest differences (and therefore lowest fit) involve comparisons between canopy height change and other measures, e.g., basal area loss (Ft=0.20, FD=1.97). Table 11 shows measures for maps compared at the quadrat (20 m by 20 m grid cell) scale. I also examined the trends in fit by shifting the spatial scale or resolution of the maps of damage (Figure 16). In three of the six map comparisons, representing the range of average difference values, the minimum difference between maps occurred at an intermediate scale of 10 m grid cell resolution. Using the maps generated from different measures of hurricane damage, I determined patch size frequency distributions (Figure 17). Regardless of the measure of damage used to define the patch of damage, the mode of the distribution is in the smallest size class, defined by a single 5 m by 5 m subquadrat (0.0025 ha). In the more specific measures of damage the distribution is more concentrated in the smaller patch sizes. For example, using percent mortality, a measure that is particularly sensitive to species distribution because of species differences in mortality, 91% of the patches are the minimum size at this spatial resolution and the largest discrete patch is 0.015 ha. With damage measures that are more general, (i.e. measures that combine different types of damage), the distribution is increasingly skewed to larger patch sizes. Patches defined by percent stem damage of any kind have 78% in the smallest size and no patch is larger than 0.0175 ha. Using percent basal area lost, the resulting patch size distribution has 72% in the smallest patch size and the largest patch reaches 0.04 ha. The most general measure of damage is the change in canopy height. This damage measure gives a distribution of patches with 26% in the smallest size (still the mode), but defines patches as large as 0.4 ha. When the frequency distribution is expressed as the proportion of the total area damaged in each patch size class, the modes are still in the smallest patch size. The one exception is when canopy damage is quantified as a decrease in canopy height (Figure 18). With this measure of damage, 56% of the total damage area occurs in patches larger than 0.004 ha. Table 11 - Measures of fit between maps of damage. The upper right half of the table presents the measured fit for a window size of one (F1) over the average fit for all window sizes (Ft). The lower half of the table presents the average difference between grid cell values (FD), with no shift in window size (20 m grid cell resolution). F1 Ft SNAP TIP BRANCH DEAD DEAD STEMS STEMS BA % BA HEIGHT
SNAP | X 0.36 0.36 0.50 0.49 0.49 0.45 0.45 0.42 0.12 | 0.68 0.58 0.80 0.77 0.84 0.80 0.65 0.79 0.40 | TIP | 0.95 X 0.48 0.52 0.53 0.46 0.42 0.66 0.57 0.09 | 0.72 0.80 0.84 0.63 0.60 0.88 0.80 0.24 | BRANCH | 0.98 0.77 X 0.46 0.45 0.29 0.26 0.53 0.41 0.09 | 0.66 0.68 0.51 0.45 0.75 0.64 0.20 | DEAD | 0.61 0.62 0.83 X 0.84 0.57 0.48 0.55 0.56 0.10 | 0.91 0.76 0.71 0.76 0.87 0.34 | % DEAD | 0.64 0.61 8.80 0.16 X 0.49 0.47 0.59 0.56 0.08 | 0.71 0.68 0.81 0.84 0.29 | STEMS | 0.59 0.70 1.14 0.53 0.63 X 0.71 0.39 0.51 0.19 | 0.876 0.58 0.76 0.46 | % STEMS| 0.70 0.84 1.27 0.70 0.70 0.31 X 0.33 0.46 0.20 | 0.55 0.73 0.48 | BA | 0.76 0.43 0.64 0.55 0.51 0.81 0.95 X 0.60 0.06 | 0.76 0.20 | % BA | 0.76 0.56 0.98 0.55 0.54 0.58 0.63 0.46 X 0.13 | 0.38 | HEIGHT | 1.60 1.88 2.00 1.71 1.78 1.39 1.34 1.97 1.62 X
FD Figure 17 - Patch size frequency distribution. Frequency of the total number of patches in each patch size. Y-axis is log scale to make the lower proportion in larger gap sizes visible. Figure 18 - Patch size frequency distribution proportion of the total area of damage in each patch size. Table 12 - T-Square Distance Sampling. Using a grid of 286 points, X is the distance from the grid point, Y is the distance to the second point. C is T-Square Index. I is Distance Index of Dispersion. z is the z value for normal distribution.
Damage Mean Mean Type X Y C z I z
Branch 6.35 7.61 0.53 2.04a 4.91 24.83a Tip up 7.70 10.21 0.57 3.81a 2.25 2.13a Snapped 7.32 9.46 0.54 2.85a 2.26 2.22a Dead 6.64 8.64 0.54 2.10a 2.27 2.23a All Stems 5.01 6.53 0.54 2.55a 2.20 1.75
a significant at p< 0.05 Both the T-Square Index (C) and the Distance Index of Dispersion (I) show a significant tendency toward clumping of damage for all measures except stem damage, which is signifi- cantly clumped only for C (Table 12). While significant, the values of the statistics were not much greater than 0.5 (C) and 2 (I), indicating small departures from random patterns. The results of the spatial pattern analysis for both PQV and BQV of the three randomly selected transects is presented in Appendix C-VII. These results are averaged and graphed in Figure 19. This analysis shows weak, but significant, peaks in variance depending on the measure of damage. Mortality shows a significant tendency toward patch spacing at 10 m, and again at 35 m. The variance shows peaks at patch spacings of 15 m and 35 m for stem damage. Basal area damaged appears to have a complex patch spacing structure with peaks of variance at 15 m, 25 m, and 35 m (Figure 19). Few clear trends in the data set were illuminated by PCA (Table 13). The first three principal components seldom accounted for more than 35% of the variance of the data set. In all analyses, the total amount of variance accounted for by the first three principal components decreases when the analysis was done using a finer spatial scale. For example, the cumulative eigenvalue for the third principal component is: 0.317, 0.270, and 0.253 respectively for spatial scales of 20 m, 10 m, and 5 m. Including the spatial component of the data set increases the cumulative eigenvalues at all three levels only slightly: 0.331, 0.293, and 0.268. Figure 19 - Spatial pattern analysis. Variance averaged for all data sets both pooling paired and block quadrat methods and transformed to a scale of 0 - 100. Error bars are standard errors of the mean. * indicates a significant (p=0.05) peak, based on the random paired quadrat variance. Dead and stems are counts, BA is basal area damaged values. The only analysis that accounts consistently for the majority of the variance is when PCA is applied to the subset of 12 damage variables. In these cases, the loadings on the first three principal components change between the three spatial scales. At the 20 m scale, the first eigenvector coefficients are highest for mortality, stem damage, and basal area damage and the percent damage for each of these measures. For these six, the eigenvector coefficients are all positive and have values between 0.34 and 0.39. The first principal component eigenvalue at this scale accounts for 47.9% of the variance and appears to be differentiating between damaged and undamaged sites. The first eigenvector coefficients at scales of 10 m and 5 m show the same trend in loading, and similar values. At the 20 m scale, the second eigenvector is loaded most heavily by the number of root breaks and branch damage (0.53 and 0.48 respectively), contrasting with the negative coefficient for bent stems (-0.597). This principal component differentiates between grid cells based on these rare damage types, and appears to pull out the few grid cells with bent stems. Only 92 stems were bent in the entire data set, and the maximum per 20 m grid cell was two (Table 10). This second principal component accounts for only an additional 8.9% of the variance of the data set. The second eigenvector at scales of 5 m and 10 m shows a different pattern of loading. In both cases, the largest coefficient is for tip-ups (-0.577 and -0.521 respectively). The next highest loadings are for snapped stems and root breaks, in both cases. The second principal component accounts for 9.4% and 9.1% of the variance at the 5 m and 10 m scale, respectively. This principal component is differentiating between types of stem damage, probably corresponding to different vegetation communities associated with 1936 cover classes. This same trend in loading is found in the third eigenvector for the 20 m scale. Here the coefficient for tip- ups is -0.560 and for snapped stems is 0.451. Table 13 - Results of principal component analysis Cumulative eigenvalues of the first three principal components. All analyses run at all three spatial scales.
Data set Scale PC1 PC2 PC3
All data 20 0.151 0.245 0.317 Damage variables 20 0.479 0.568 0.656 Dummy variables 20 0.140 0.229 0.302 Include spatial 20 0.153 0.248 0.331
All data 10 0.122 0.215 0.281 Damage variables 10 0.447 0.538 0.625 Dummy variables 10 0.116 0.207 0.270 Include spatial 10 0.119 0.215 0.293
All data 5 0.116 0.194 0.258 Damage variables 5 0.433 0.528 0.615 Dummy variables 5 0.109 0.191 0.253 Include spatial 5 0.109 0.191 0.268
When the data set is separated into subsets based on specific categorical variables, some additional patterns emerge. The region of the HRP with < 20% cover in the 1936 photos has consistently higher cumulative eigenvalues for the first three principal components. This region of the plot is a steep slope and ridge top. At the 20 m and 10 m scale, high loadings also occur for elevation and slope. At the 10 m and 5 m scale, damage measures of mortality, stem damage, and basal area damaged also have high loadings. At all three spatial scales, the eigenvectors are loaded to number of stems. Separating the data set into topographic position categories of valleys and ridges, the presumed extremes in the exposure gradient, also results in higher cumulative eigenvalues. For all valley grid cells, the first principal component shows the same pattern as the analysis of all damage variables. That is, the highest eigenvector coefficients, at all three scales, are general measures of damage: mortality, stem damage, and basal area damage. For the subset of ridge grid cells, this same pattern in loadings is observed, with the additional high coefficients of snapped stems. On ridges, stems may either snap, or not be damaged, and this pattern is reflected in the more general measures of damage. CCA shows increasing cumulative eigenvalues for the third canonical correlate with finer spatial scales. For the entire data set, with dummy variables for the categorical variables, the cumulative eigenvalues are: 0.811, 0.815, and 0.835, for the 20 m, 10 m, and 5 m scales respectively (Table 14). However, the correlation coefficients between the environmental variables and damage measures show the opposite trends with changing spatial scale. The correlation coefficients for the first canonical correlates are: 0.891, 0.738, and 0.671, respectively. Table 14 - Results of canonical correlation analysis. Correlation coefficients and cumulative eigenvalues of the first three canonical correlates. All analyses run at all three spatial scales.
correlation coefficient eigenvalues Data Set Scale CC1 CC2 CC3 CC1 CC2 CC3
Abiotic and damage 20 0.528 0.355 0.312 0.507 0.696 0.837 Biotic and damage 20 0.878 0.807 0.651 0.498 0.775 0.883 All data and damage 20 0.883 0.812 0.670 0.476 0.737 0.847 Abiotic dummy 20 0.548 0.447 0.411 0.308 0.487 0.632 All data and dummy 20 0.891 0.821 0.681 0.461 0.708 0.811
Abiotic and damage 10 0.433 0.235 0.164 0.663 0.831 0.910 Biotic and damage 10 0.718 0.601 0.464 0.489 0.749 0.875 All data and damage 10 0.731 0.608 0.479 0.479 0.723 0.847 Abiotic dummy 10 0.450 0.284 0.224 0.472 0.635 0.733 All data and dummy 10 0.738 0.614 0.485 0.463 0.700 0.815
Abiotic and damage 5 0.332 0.194 0.089 0.689 0.907 0.951 Biotic and damage 5 0.658 0.484 0.339 0.572 0.801 0.898 All data and damage 5 0.668 0.486 0.360 0.549 0.758 0.859 Abiotic dummy 5 0.353 0.225 0.128 0.568 0.781 0.847 All data and dummy 5 0.671 0.489 0.363 0.532 0.736 0.835
The canonical environmental variables are correlated to stems, basal area, and abundance of Prestoea montana; at all three spatial scales. The canonical damage variables are correlated to stem damage, basal area damage, and branch damage. Correlations between the environmental variables and the canonical damage variables include number of stems, basal area, and abundance of Prestoea montana, Dacryodes excelsa, Manilkara bidentata, and Matayba domingensis (Appendix C-IX). Separating the data set by categorical variables results in low or insignificant correlation coefficients (Appendix C- X). In categories of both soil and topography, cover class tended to have the largest coefficient in, and have the highest correlation to, the canonical variable of damage, indicating its importance in influencing damage. When the data set is categorized by cover class, elevation is the most consistent variable highly correlated to the canonical variable of damage. Finally, I examined the relative importance of biotic variables versus abiotic variables in influencing damage. The results show that biotic variables are much more highly correlated with damage (Figure 20). At all three spatial scales, the multivariate correlation between biotic variables (presence of specific species) and damage is higher than that between abiotic variables (plot variables of topography, edaphic characteristics and disturbance history) and damage, and when all variables are included in the analysis, the correlation increases only slightly above that of the biotic variables alone. Canonical correlation coefficient values increased as the grid cell size increased from 5 m to 20 m resolution. Figure 20 - Correlation between environmental factors and damage. Canonical correlation calculated at three grid cell sizes and damage variables correlated with only abiotic variables, only biotic variables, and all variables. Abiotic, biotic, and damage variables as defined in Table 10.
DISCUSSION
Different measures of hurricane damage severity give different spatial patterns of damage. In the HRP these patterns of damage vary at the scale of the entire plot, reflecting differences in tree communities, and at small scales (tens of meters) due variations in factors that control the establishment and grow of individual tree species. The pattern of damage differs between the north and south ends of the grid, with stem damage concentrated in the north and branch damage concentrated in the south. The north end of the grid is known to have been subjected to clear cutting in the 1920's and was categorized as having only 40-80% cover in 1936 (based on aerial photographs). The earlier successional tree community in this region of the grid (dominated by Casearia arborea) is more susceptible to stem damage (Figure 15). The southern end of the grid is composed of a primary forest tree community, with the canopy dominated by Dacryodes excelsa, Sloanea berteriana, and Manilkara bidentata. These species are more resistant to stem damage and mortality, but tend to shed branches in a hurricane. This pattern is reflected in Figure 15B. The response of these species to hurricane winds has been reported by Dallmeier et al. (1991), Walker (1991), Basnet et al. (1992), Walker et al. (1992), and Zimmerman et al. (1994). This characteristic resistance of primary forest tree species to stem damage, and the susceptibility of pioneer species, has been reported for other wind disturbances (Whitmore 1974, Putz et al. 1983, King 1986, Webb 1986, Veblen et al. 1989, Nelson et al. 1994). The tendency toward loss of branches, rather than more severe stem damage, may explain the lack of fit between maps of canopy height and maps of other measures of damage. Loss of branches disrupts the canopy and may create gaps, without corresponding damage to stems. At the scale of the entire plot, (16 ha), disturbance history may be the best predictor of patterns of damage, since this influences the resultant tree communities and canonical variables of damage are correlated to the distribution of primary forest tree species (Appendix C-IX). At finer scales, heterogeneity increases between maps generated by different measures of damage severity. This may reflect the differences in species' response to hurricane winds, and the fine scale variation in the distribution of trees. Damage is clumped significantly and the patch sizes are concentrated in the smallest size measured (0.0025 ha), with all measures of damage. Spatial pattern analysis indicates variations in the spacing of these clumps relative to the measure of damage. Measures of damage that are associated most strongly with species differences, e.g., mortality, show simpler patch spacing structures. More general measures of damage, e.g., percent basal area lost, which incorporate multiple types of damage (in this example, mortality and all types of stem damage), show more complex patterns of patch spacing. These complex patterns of patches probably reflect both overlapping patterns of tree species distribution and the skew toward occurrence of larger patches when more general measures of damage are used. This analysis emphasizes the increasing heterogeneity at a fine spatial scale. GIS-based terrain models often rely on remotely-sensed data that result in grid cell sizes of 30 m by 30 m or larger. Terrain models at this resolution may miss much of the dynamics of disturbance and recovery from a hurricane impacting a montane landscape. However, modeling the landscape at a scale of 5 m by 5 m grid cell may be inefficient in terms of data storage and processing. With patch spacings of 10 to 15 m, terrain models based on grid cells of 10 m by 10 m offer a reasonable compromise and should capture much of the fine scale patch structure, at least in the HRP (Figure 18). Although many researchers have noted that both abiotic and biotic factors influence patterns of wind damage (Bromley 1939, Smith 1946, Stoeckeler & Arbogast 1955, Neustein 1971, Allen 1992, Boose et al. 1994), little effort has been made to determine the relative importance of biotic versus abiotic factors, particularly at small spatial scales. Boose et al. (1994) reported on the factors influencing patterns of disturbance on larger scales, from continental (1000 km) to stand (1 km), for Hurricane Hugo in Puerto Rico and for the 1938 hurricane in New England. At their finest scale (stand), they reported wind gusts, variation in exposure, and variations in species susceptibility as the factors controlling patterns of damage. At the scales investigated in this study, (25-400 m2), almost the entire variance explained by all variables describing the plot can be attributed to the biotic variables. This control by biotic variables could be attributed to weak abiotic gradients in this less severe montane landscape. However, Basnet et al. (1992) found a similar association between species distribution and damage in a steeper watershed of the LEF. In their study, exposed ridges suffered less damage due to the presence of Dacryodes excelsa and other primary forest species. An alternative explanation for the control by biotic variables is that these variables become more important at finer spatial scales. Foster (1988) predicted a shift from variations in storm intensity and abiotic factors controlling severity of damage at large scales, to biotic control of damage at smaller scales. The results of this study, a single storm event, when taken with the work of Boose et al. (1994), support this prediction. Figure 21 presents a conceptual diagram of the interactions among these controlling variables, with a relatively short (one hurricane cycle) temporal scale. Topography, climate, and disturbance history all influence the gradients of abiotic factors across the landscape. These factors influence the distribution of individual tree species, and the resulting biotic communities, although the results of this analysis do not support the ability to use these abiotic factors to predict tree distribution and subsequent damage. These biotic factors, in turn, influence the impact of disturbance, mitigate mesoclimate, and create microclimates. For each new hurricane, disturbance history changes. At longer spatial scales, topography and climatic disturbance regimes may change also. Figure 21 - Interactions among disturbance, abiotic gradients, and biota; for a single hurricane disturbance. The spatial pattern of hurricane damage suggests that catastrophic wind disturbance is similar to background treefall gap formation, since patches of damage are concentrated in the smallest sizes. However, hurricane damage also results in extensive defoliation, an impact not captured in any of the measures examined in this chapter. This defoliation has several effects: 1) greater shifts in abiotic gradients, such as light, than would be associated with a treefall gap (Veblen et al. 1989, Fernandez & Fetcher 1991, Turton 1992, Walker et al. 1992), 2) system-wide pulses of litter which will influence the nutrient availability during recovery (Lodge et al. 1991, Whigham et al. 1991), and germination and seedling survival (Guzmán-Grajales & Walker 1991, Everham et al. in press) and 3) shortages of seed and seed dispersers over large regions (Synder & Synder 1979, Zamore 1981, Boucher 1990, Yih et al. 1990, Lynch 1991, Wiley & Wunderle 1994). These effects, together with the occasional much larger patches of damage created by a hurricane insure unique dynamics of recovery (Foster 1988). The mixture of patch sizes and the elements of disturbance not associated directly with patch size make Denslow's (1980) predictions of a relationship between disturbance patch size and the tree life histories difficult to extend to hurricane disturbance. In hurricane-prone areas, species may be adapted to other aspects of the disturbance, such as defoliation, that are not related to gap size. The results of this study indicate the importance of tree community data, previous disturbance history, and the influence of this disturbance on the tree communities. The ability to predict patterns of severity of damage at scales of tens of meters is dependent on detailed data of the distribution of species and their susceptibilities to wind disturbance. These predictions are critical for understanding the long-term stand- level dynamics in hurricane prone areas.Return to the Table of Contents