CONSERVATION OF MOMENTUM AND ENERGY IN
COLLISIONS
GOAL
The goal of this work is to investigate the relationship between total momentum (and energy) of two carts before and after elastic and inelastic collisions.
PREREQUISITES
R.D. Knight, Physics, Chapters 9, 10.
EQUIPMENT
Two motion censors
Air track with blower
Two air track carts
Scale
THEORY
The momentum of an object is the product of its mass and its velocity. According to the law of Conservation of Momentum, the total initial momentum of the system (the sum of momenta of all objects prior to a collision) equals to the total final momentum of the system (the sum of momenta of all objects after the collision) if there are no external forces acting on the system. Total momentum is conserved during both elastic and inelastic collisions. The law is illustrated on the picture below for the binary collision.
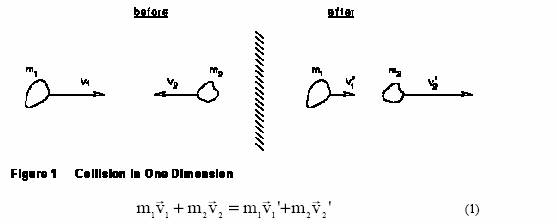
At the same time, the mechanical energy (kinetic energy plus
potential energy) is conserved only in the perfectly elastic collisions. During
the inelastic collision we have deal with transformation of mechanical energy
into the heat.
PROCEDURE
1. Setup the carts for elastic collision attaching the rubber to one of the
cart.
2. Use the scale to measure the mass of each cart and record the values.
3.
Start your
4. Figure out which graph (upper or lower) corresponds to left (right) sensor. To do that block one of the sensor and gently initiate collision of carts. The blocked sensor will produce horizontal line on the screen. NOTE, that sensors and reflection screens on carts have to be appropriately mounted. In case of the absence of signal on the screen check sensors and reflection screens – you probably have to change the position of the sensor or to rotate the reflection screen.
5.
Practice a few times to
record collision event. Stop
6. Repeat elastic collision three times. Every time record data (carts’ velocities) in the Table 1.
7. Setup the carts for inelastic collision attaching the cork to one of the
cart.
1. Repeat items 2-7 for inelastic collision recording your data in Table 2.
Table 1. Elastic Collision.
Mass of the left cart: ___________________________________
Mass of the right cart: __________________________________
|
N of trial |
V1i (m/s) |
V1f (m/s) |
V2i (m/s) |
V2f (m/s) |
Pi (kg·m/s) |
Pf (kg·m/s) |
Ei (J) |
Ef (J) |
|Pi-Pf| |
|Ei-Ef| |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Table 2. Inelastic Collison.
Mass of the left cart: ___________________________________
Mass of the right cart: __________________________________
|
N of trial |
V1i (m/s) |
V1f (m/s) |
V2i (m/s) |
V2f (m/s) |
Pi (kg·m/s) |
Pf (kg·m/s) |
Ei (J) |
Ef (J) |
|Pi-Pf| |
|Ei-Ef| |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
ANALYSIS
1. Make all necessary calculation to fill both Tables completely.
2.
Explain your results (mainly content of two last
columns in each Table).