Introduction to Measurement and
Error Analysis.
The
Goal
You have to learn how
to make the measurements of one of the basic physical quantity - length. You will
also get an introduction to measurement errors associated with these
measurements.
Prerequisites
“Physics for
Scientists and Engineers” R.D. Knight: Chapters 1.9.
Equipment
-
Cardboard box
-
Meter Stick
Procedure
You primary goal is to
calculate the volume of the cardboard box.
To make calculations you have to measure box’s width, depth, and height.
The volume can then be determine as a product
V
= width x depth x height
However the box is not perfect. For example, its width is slightly
different depending at which place you are doing your measurement. To ensure
more reliable data make at least five measurements of each quantity at
different places. Do not measure one variable (width, for example) five times
consequently to obtain more reliable results. Fill in appropriate columns of tables
(for the width the table is shown below) using SI standard units and numbers in
scientific notation.
|
Width |
Error
of measurement |
|
2.37 x 101 m |
1.0 x 10-2 m |
|
|
|
|
|
|
|
|
|
|
|
|
Note, that experimental uncertainties (errors of
measurements) always exist and your prime function, as a scientist, to minimize
them. Try to answer the following questions:
-
What is the source of errors during single
measurement of the length?
-
What factor does determine the value of
that error?
-
Can we minimize that error? What do we
have to do for that?
Determine the minimal values of your errors of measurements
and fill in the right columns in appropriate tables. Note, that you have no
ways to minimize these errors – they are simply determined by the procedure and
tools used in the process of measurement. These
limitations on the precision of a measurement are commonly called scale errors
or scale uncertainties.
Scale uncertainty is
a limiting factor in the precision of a measurement. It is due to the fact that
a measuring scale can have only finitely many divisions. It is reasonable (and
expected) to estimate one digit between the finest markings on the scale (if
possible).
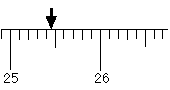
Analysis
of data
1. Examine
the data in left column of the “Width” table. Note, that particular numbers are
slightly different due to imperfections of the box. To estimate the average
width of the box calculate the mean value of the width (just arithmetic
average) as
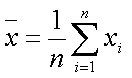
where n is the number of measurements. This
value gives as rather good
approximation of
the overall cardboard box width.
2. Now
estimate how far away from this value our particular results of measurements
are with the help of standard deviation σ
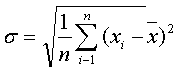
Standard deviation allows us to estimate uncertainty interval for the mean
value of a set of measurements in the form
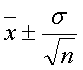
3. Now you have two different estimates for the
errors:
- scale uncertainty
- ![]()
To make final decision about errors you
can simply pick up the largest
one.
3. Repeat
previous steps for the length and depth.
4. Calculate
the volume of the cardboard box using the mean values for width, length, and
depth.
5. Estimate
the error of the volume using the following simple rules:
·
When adding or subtracting measurements, add their absolute uncertainties. Symbolically,
if the most probable value of the sum of two measurements x
and y
is s
(s
= x + y), and if Δx and Δy are the
absolute uncertainties of x and y respectively, then the
uncertainty in s,
Δs, is: Δs= Δx+ Δy
·
When multiplying or dividing measurements,
add their relative uncertainties. Symbolically, if x and y
are two measurements, and if their absolute uncertainties are Δx and Δy, then the relative uncertainty in x
is 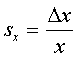 and the relative
uncertainty in y
is
and the relative
uncertainty in y
is 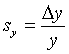 . The relative uncertainty in x·y (or x/y) is
. The relative uncertainty in x·y (or x/y) is
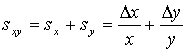 . Finally we can find the absolute uncertainty for s,
. Finally we can find the absolute uncertainty for s, ![]()
·
The relative
error in ![]() is relative error in x
divided by 2.
is relative error in x
divided by 2.
Lab
Report Preparation
Write an appropriate
lab report. It has to contain
1. Your
name and name of all your partners, date and time of work.
2. Name
of the lab (title).
3. Goal
of the lab.
4. List
of equipment used in the lab.
5. Obtained
data with detailed analysis.