CENTRIPETAL FORCE
GOAL
To verify
the second
PREREQUISITES
R.D. Knight, Physics for scientists and engineers, chapter 7.
EQUIPMENT
Centripetal Force Apparatus
Slotted Mass Set
Vernier Caliper
Stopwatch
Scale
Ruler
THEORY
An object moving in a circle of radius r at constant speed v (and a period of motion T)
v=2π·r/T,
has an acceleration whose direction is toward the center of the circle and whose magnitude is
ar=v2/r.
According to
Fnet=m·ar=mv2/r
This net force must be directed toward the center of the circle.
PROCEDURE
|
|
Trial 1 |
Trial 2 |
Trial 3 |
Trial 4 |
|
Radius of rotation, r (m) |
± |
± |
± |
± |
|
Displacement mass, md (kg) |
|
|
|
|
|
Displacement force, Fd (N) |
|
|
|
|
|
Heavy mass, m (kg) |
± |
|||
|
Period of rotation, T (s) |
|
|
|
|
|
Speed of rotation, v (m/s) v=2π·r/T |
± |
± |
± |
± |
|
Force from F=m·ar=mv2/r |
|
|
|
|
|
Difference between forces (%) |F-Fd|/F*100% |
|
|
|
|
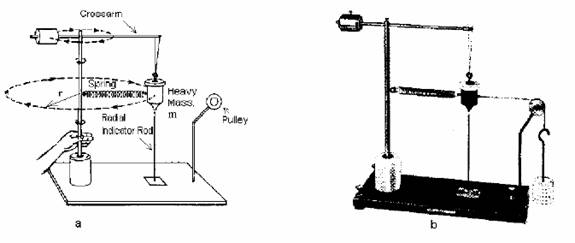
- Determine
the value of the heavy mass m with a scale balance. Note, that you have to
do that measurement only one time. Record that value in fifth raw of the
Table.
- Disconnect
the spring from heavy mass. Adjust the radius of rotation to a minimum
possible value. Tighten the knurled screw on top of the vertical shaft.
Measure the radius of rotation and record data in the Table. Adjust the radial
indicator rod to be vertically under the heavy mass m and fix its position. Connect the spring to the heavy mass m.
- Connect
hanger to heavy mass m via a
string over the pulley. Add mass to hanger until the radial indicator rod
is aligned vertically with the heavy mass m. Record the displacement mass md and displacement force Fd=md·g
in the Table. Remove hanger, displacement mass, and string from heavy mass
m. Rotate the system by applying
torque with your fingers on the knurled poetion of the shaft. With a
little practice the rotation rate can be adjusted to keep the heavy mass m passing directly over the radial
indicator rod. Measure the time necessary for 5-10 rotations. Calculate
the period of rotation T and
record it in the Table.
- Repeat
all previous steps for the maximum possible radius of rotations.
- Repeat
all previous steps for two arbitrary values of the rotation radius between
minimum and maximum values.
ANALYSIS
1. Make all necessary calculation to fill the Table completely.
2. Why the difference between two forces is rather large? Give your explanation.